Supóngase una urna con canicas blancas y negras que tienen grabada una letra A o Z. De tal forma que la composición de la urna es:

Experimento. Extraes una canica de la urna.
1.- Evento A: Obtener una canica negra P(A) = 6/11
2.- Evento B: Obtener una canica con letra A. P(B) = 8/11
3.- Evento C. A⋂N Obtener una canica que tenga la letra A y sea de color negro. P(C) = 5/11
4.- Evento D: Obtener una bola negra suponiendo que tenga grabada la letra A
Esto se representa N/A y P(N/A) = 5/8
El punto 4.- Se define como probabilidad condicional y se lee:
La probabilidad de N dado A.
Es fácil verificar que dicho resultado corresponde a evaluar la siguiente expresión

De aquí llegamos intuitivamente al concepto de probabilidad condicional y se define de la siguiente forma:
Definción
Si los sucesos A y B pertenecen al mismo espacio muestral S y si P(A) ≠ 0, entonces la probabilodad condicional de B respecto de A, designada por P(B/A), se define como:

Ejemplos:
1.- Experimento: Lanzar un dado
Evento : Número mayor que 3 dado que el resultado es un número par.
Solución.
Ω = S = {1, 2, 3, 4, 5, 6} Espacio muestral
A = {2, 4, 6} Resultado pares
B = {4, 5, 6} Mayores que 3
A⋂B = {4, 6} Conjunto de resultados pares mayores que 3.
a) Intuitivamente 2/3
b)
- Fórmula P(B/A)

Teorema de Bayes
Supóngase el siguiente juego:
Sea 2 urnas A1 y A2, la A1 con 8 canicas blancas y 2 negras; la A2 con 3 blancas y 7 negras.
Si se ganan $5,000 cuando se extrae una canica blanca ¿Cuál es la probabilidad de ganar este juego?
Solución.
Las formas de extraer una canica blanca es:
- P(B) = P(A1 ⋂ B)
- P(B) = P(A2 ⋂ B)
P(B) = P(A1 ⋂ B) U P(B) = P(A2 ⋂ B)
P(B) = P(A1 ⋂ B) + P(A2 ⋂ B)
P(B) = P(A1) P(B/ A1) + P(A2 P(B/ A2)
Como calcular estas probabilidades.

Ahora supóngase que se ha jugado una vez y hemos Ganado ¿Cuál es la probabilidad de que se haya elegido la urna A1?
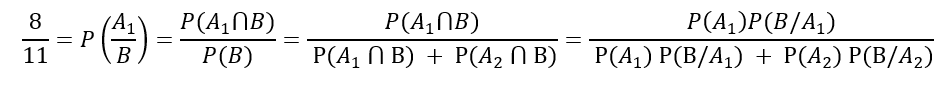
¿La probabilidad de que sea de A2?
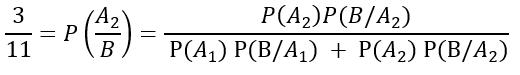
Sean eventos mutuamente excluyentes que ocupan todo el espacio muestral S. Si cada uno de estos eventos tienen probabilidad No nula y uno de ellos debe ocurrir, entonces para todos evento B en el espacio muestral S:

Finalmente

