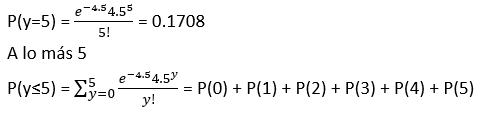Modelo → Explicar fenómeno y conducta.
- Determinista → permite establecer que ciertas condiciones causan un estado subsiguiente.
- Probabilista → si dadas ciertas condiciones iniciales ocurrieran ciertos estados con tales y tales probabilidades. Es decir, dadas las condiciones iniciales en modelo probabilista permite deducir su distribución de probabilidades de posibles estados pueden ser siguientes, que con valores de una variable aleatoria.
I.- Modelos de probabilidad Discretos.
II.- Modelos de probabilidad Continuos.
Modelo Bernoulli
Se aplica a variables aleatorias que puedan asumir solo 2 valores.
Resumiendo.
Sea X con 2 únicos valores x1=1, x2=0 y f(x1) = p y f(x2) = q = 1-p; entonces

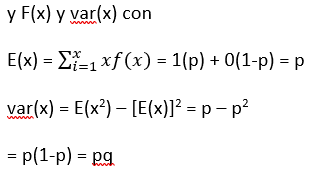
Condiciones
- Ensayos independientes
- Cada uno con 2 únicos resultados
- La probabilidad de cada resultado permanece constante de ensayo a ensayo.
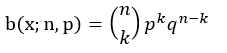
x=0,1,…,n
p=número de éxitos
n=número total de eventos
Distribución multinominal
Supóngase un experimento capaz de dar k resultados posibles mutuamente excluyentes, E1, E2, E3, …, Ek, con probabilidades respectivas p1, p2, p3, …, pk, donde p1+ p2+ p3+ …+ pk,=1. Si se repite este experimento n veces independientemente, y los p´s permanecen constantes, la probabilidad de obtener x1 ocurrencia de E1, x2 ocurrencia de E2, …, y xk ocurrencia de Ek, dado que x1+x2+…+xk=n es:
f(x1,x2,…,xk; p1, p2, p3, …, pk)=

Binomial
N grande en relación a n o n pequeña en relación a N.

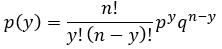
Ejemplo
Supóngase un lote de 300 fusibles eléctricos que contienen 5% de defectos. ¿Probabilidad de encontrar al menos 1 defectuoso en una muestra de 5 fusibles?
P(al menos un defectuoso)=1-p(0)
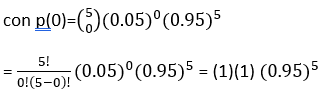
P(al menos un defectuoso)= 1- (0.95)5= 1-0.774 = 0.226
TEOREMA.
Sea Y una v.a. binomial, basada en n pruebas y con la probabilidad de éxito p. Entonces μ=E(y)=np y σ2 = V(y) = npq.
Distribución Geométrica
Pruebas idénticas e independientes.
- Dos posibles resultados E o F.
- Probabilidad de éxito igual a p y es constante para cada prueba.
- La v.a. Y es el número de la prueba n la geométrica cual ocurre el primer éxito.
Entonces, el experimento consiste en una serie de pruebas que termina al obtener el primer éxito.
Definición
Una v.a. Y tiene una distribución de probabilidad geométrica, si y solamente si
p(y) = qy-1 p y=1,2,…, 0 ≤ p ≤1
Teorema. Sea Y una v.a. con una distribución geométrica. Entonces
μ = E(y) = 1/p y σ2 = v(y) = 1-p/p2
Distribución Binomial Negativa
- Ensayo o prueba independiente, idénticas.
- Sólo dos posibles resultados E o F.
- Probabilidad de éxito igual a p y es constante para cada prueba.
- Interesa el número de la prueba en la cual ocurre el segundo, el tercero o el cuarto éxito.
- Y es una v.a., número de la prueba en la que ocurre o representa el r-ésimo éxito (r=2,3,4,…)
Definición
Una v.a. Y tiene una distribución de probabilidad binomial negativa si y solo si
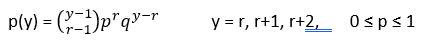
TEOREMA.
Si Y es una v.a. con distribución binomial negativa, entonces:

Distribución Hipergeométrica
- La población o conjunto donde se hace el muestreo consta de N individuos, objetos o elementos (una población finita).
- Cada individuo puede caracterizarse como un éxito o fracaso, y hay M éxitos en la población.
- Se elige una muestra sin remplazo de n individuos, de tal forma que sea igual de probable seleccionar cada subconjunto te tamaño n.
La variable aleatoria de interés es y=número de éxitos en la muestra. La distribución de probabilidad de y depende de los parámetros n, M, y N; de tal forma que se desea obtener
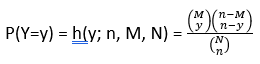
Definición
Si y es el número de éxitos de una muestra completamente aleatoria de tamaño n de una población formada por M éxitos y (N-M) fracasos, entonces la distribución de probabilidad de y, llamada distribución hipergeométrica, está dada por:
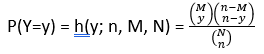
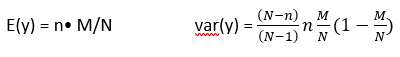
Ejemplo:
Cinco ejemplares de una población animal, considerados en vía de extinción en cierta región, se han atrapado, marcados y puestos en libertad para que regresen a su población original. Después de esto se elige una muestra de tamaño 10. Si y= número de animales marcados en la segunda muestra. Si hay en realidad 25 animales de este tipo en la región ¿Cuál es la probabilidad de que a) y=2, y b) y≤2?
NOTA: n=10, M=5 (animales marcados en la población), N=25; así que
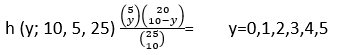
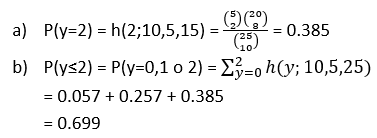
Distribución Poisson
Definición. Se dice que una v.a. tiene una distribución de Poisson si su f.d.p. de y es:

NOTA: λ con frecuencia es una tasa por unidad de tiempo o por unidad de área.
Ejemplo
Sea Y la cantidad de ostras de cierto tipo que caen en una trampa durante determinado periodo. Supongamos que Y tiene una distribución de Poisson con λ= 4.5 criaturas (el artículo “Dispersal Dynamics of Bivalve Gemma Gemma on a Patchy Enviromental” sugiere este modelo). La probabilidad de una trampa contenga exactamente cinco criaturas es: