Cuando una variable aleatoria X es definida como continua, tiene un número incontable de posibles valores. La F.D.A. (f.d.p.a.) de X sería entonces continua en el sentido de que su gráfico es suave. Debido a la continuidad, la probabilidad de que X asuma cualquiera de sus posibles valores en cero; así aunque la noción de f.d.p de v.a. discretas puede aplicarse, no da resultados útiles.
En su lugar, representamos f(x) como una función de densidad de distribución. Este nombre se basa en el hecho de que consideramos una función de densidad como la velocidad (la derivada de f.d.p.a) con que se acumularía la probabilidad si pasáramos rápidamente de la izquierda a la derecha sobre el eje de los valores de la variable X.
Una función de densidad es una medida de la concentración de probabilidad dentro de un intervalo. Esta probabilidad puede interpretarse como un área (una integral) bajo la curva de f(x), llamada curva de densidad, limitada por las ordenadas en los puntos finales de su intervalo.
Más precisamente, si X es una v.a. continua la probabilidad de que tome valores entre a y b, con a<b, puede representarse por P(a<x<b) y es igual al área bajo la curva de f(x) encerrada por ordenadas establecidas en a y b.
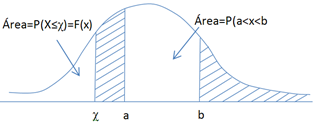
Obsérvese que F(x) = P(x ≤ χ)
También obsérvese que f(x) puede interpretarse como la velocidad de cambio de F(x).
Distribución Normal
Sea x una v.a. continua. Entonces, una distribución de probabilidad o función de densidad de probabilidad (f.d.p.) de x es una función tal que para cualesquiera dos números a y b, con a ≤ b
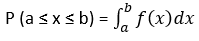
Esto es, la probabilidad de que x tome un valor en el intervalo [a,b] es el área bajo la curva, de la gráfica de la función de densidad.
Para que f(x) sea una fdp legítima, debe satisfacer las siguientes dos condiciones
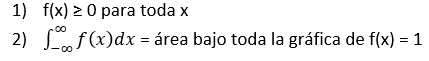
Ejemplo
Suponga que al abordar el microbús para ir a la escuela, se tiene un tiempo de espera máximo de 5 minutos. Debido a variaciones en la hora de salida, no siempre se llega al mismo tiempo a la parada de la esquina, por lo que el tiempo de espera x al siguiente microbús es una v.a. continua. El conjunto de posibles valores de x es el intervalo [0,5].
Una posible pdf para x es:


Uso de F(x) para calcular probabilidades.
Sea X una v.a. continua con f.d.p. f(x) y f.d.c.
P(x>a) = 1-F(a)
y para dos números a y b cualesquiera, tales que a<b
P(a ≤ x ≤ b) = F(b) – F(a)
Ejemplo
Suponga una v.a. con f.d.p.
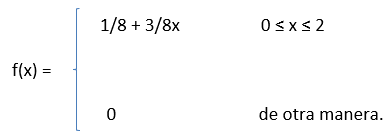
Entonces, para cualquier x entre cero y 2.
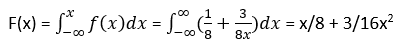
La probabilidad P(1 ≤ x ≤ 1.5) se obtiene por
P(1 ≤ x ≤ 1.5) = F(1.5) – F(1.0)
= [1/8/1.5) + 3/16(1.5)2] – [1/8(1) + 3/16(12)]
= 11/16 = 0.688
NOTA: Una vez que se obtiene la f.p.a. (f.d.a) se puede calcular con facilidad cualquier probabilidad donde intervenga x, sin más integraciones.
Definición
El valor esperado o valor medio de una v.a. x continua con fdp, f(x), es:

Ejemplo
Dada una v.a x con fdp:

Un maestro universitario nunca termina su clase antes de que suene la campana y simpre termina su clase a menos de 2 minutos después de que suena la campana. Sea x=tiempo que transcurre entre la campana y el término de la clase, y suponga que la pdf es:

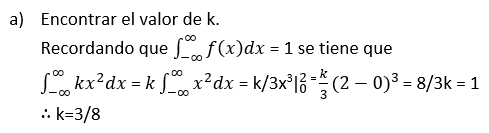


Un maestro universitario nunca termina su clase antes de que suene la campana y siempre termina su clase a menos de 2 minutos después de que suena la campana. Sea x=tiempo que transcurre entre la campana y el término de la clase, y suponga que la pdf es:



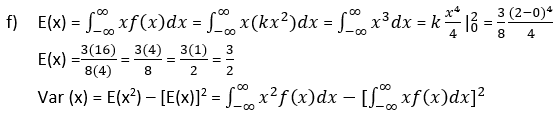
Un editor de obras asegura que sus libros están libres de errores tipográficos y la probabilidad de que cualquier página dada contenga al menos uno de tales errores es de 0.005 y los errores son independientes de página a página. ¿Cuál es la probabilidad de que una de sus novelas de 400 páginas contenga?:

Suponiendo que el 80% de todos los ejemplos de un texto en particular pasan con un éxito una prueba de resistencia de la encuadernación. Sea x el número de entre 20 ejemplos seleccionados al azar que faltan en la prueba.

Distribución Normal
General y Estandarizada
Se dice que una v.a. X tiene una distribución normal general:
- Si es continua
- Si para esa variable existen las constantes
- μ; -α < μ < α
- σ; σ > 0
y su función de densidad de probabilidades está dada por la siguiente expresión:
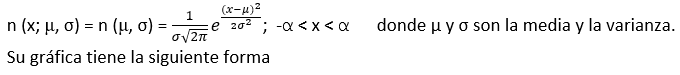

Sus parámetros son μ y σ en el sentido de que el área bajo su curva de densidad (probabilidad normal) está definida completamente por los valores de μ y σ
Analizando algunos aspectos geométricos de esta curva se tiene:
- La curva que representa a f(x) se denomina “Campana de Gauss” y es simétrica respecto a μ, X toma valores entre –α y +α
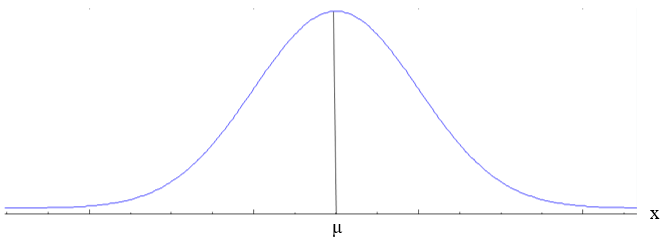
2. En μ ± σ ocurren puntos de inflexión.
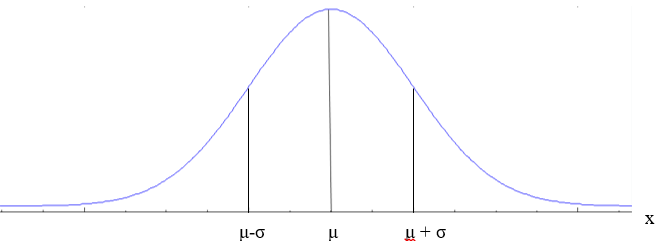
3. El área bajo la curva suma 1.
P(μ-σ < x < μ+σ) = 0.68
P(μ-2σ < x < μ+2σ) = 0.915
P(μ-3σ < x < μ+3σ) = 0.997

4. La curva es asintótica en el eje X

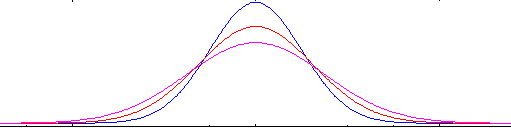
6. Un cambio de μ desplaza la curva en μ espacio:

7. Para cada valor de μ y σ existe una curva normal
Modelo Normal Estándar
Se dice que una distribución normal es de forma estándar si su media es cero y su varianza 1, de la función de densidad de la normal general, puede verse que la f.d.p. de la variable normal estándar, z, debe ser
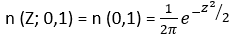

de tal forma que esta transformación de x en z reduce la x a unidades en términos de desviaciones estándar alejadas de la media. Entonces, dado un valor de X, el correspondiente valor de z nos dice cuan alejada está x de su media μ y en que dirección en términos de su desviación estándar.
Distribución Normal Estándar
Distribución de referencia con valores en tablas, donde Ф(z) = P(Z≤z)
Ejemplo
Obtener las siguientes probabilidades.
a) P(z ≤ 1.5)
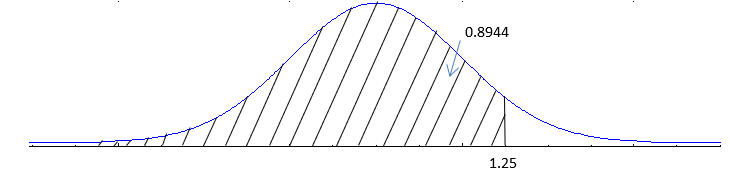
b) P(z > 1.25)
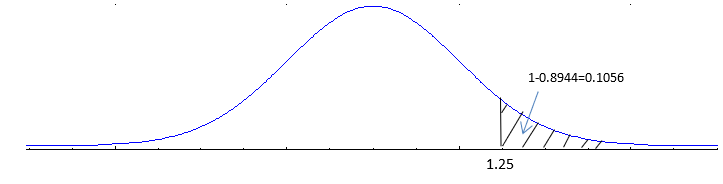
c) P(z ≤ -1.25)
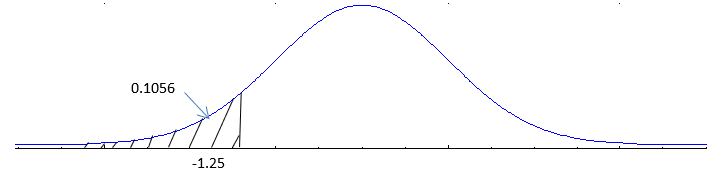
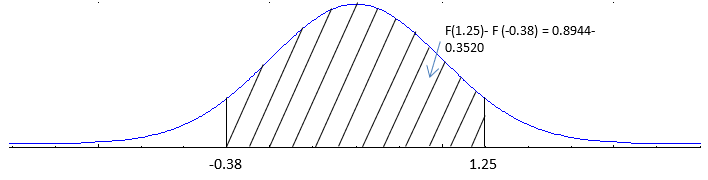
d) P(-0.38 ≤ z ≤ 1.25)