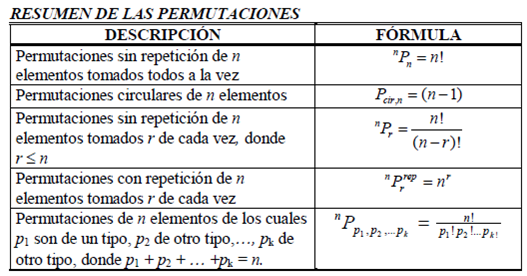
Cada uno de los arreglos formados con 2 objetos distinguibles da lugar al añadir uno nuevo distinguible de todos los anteriores, a 3 arreglos de 3 símbolos.
De aquí se puede inferir el siguiente resultado:
Dados n símbolos distinguibles entre sí, designemos con Pn el número de arreglos distinguibles que pueden obtenerse a partir de ellos.
Entonces:
Teorema (Permutación)
- El número de n símbolos diferentes es igual a Pn = n! = 1*2*(n-1)*n
Demostración:
3 objetos, 3 posiciones

1° 3 formas A2° 2 formas B3° 1 forma C
A*B*C = 3*2*1 = 6 formas.
2. Suponiendo que no todos los n son distinguibles. Para esto supongamos que los 2 primeros cubos no son distinguibles. Entonces debemos eliminar de las n! permutaciones aquellas que solo difieran por el intercambio de los 2 símbolos iguales:
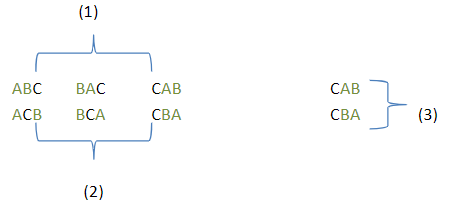
De esto podemos llegar a que
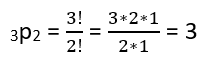
Teorema 1
Si se tienen n símbolos de los cuales k son indistinguibles entre sí y los restantes n-k son diferentes (entre sí y de los primeros k), entonces el número de arreglos distinguibles que pueden formarse con los n símbolos es n!/k!. Esto es:
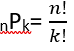
NOTA: Como k= n-r entonces se tiene

Este teorema puede generalizarse a:
Teorema 2
Considérese n símbolos agrupados en r clases, las cuales contienen k1, k2, …, kr símbolos, respectivamente, de modo que los elementos de cada clase sean indistinguibles entre sí, pero distintos de las demás clases, y donde k1+ k2+ …+kr =n. Entonces el número de arreglos distinguibles que pueden formarse resulta ser:

