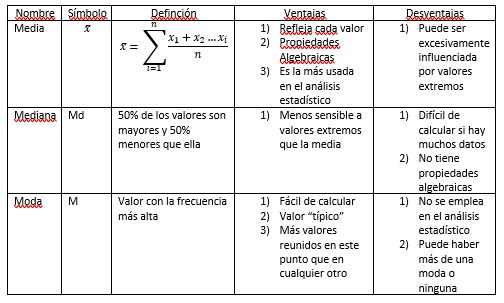
Valores “promedio” que describen todo un conjunto de datos. Se utilizan principalmente la media aritmética, la mediana, la moda y el rango medio.
Media aritmética
Si X1 X2 …. Xn constituyen una muestra de n observaciones, la media aritmética se define de la siguiente manera:

Mediana
Es el valor que ocupa la posición central en un conjunto de datos ordenados. El 50%de las observaciones son mayores que este valor y el otro 50% son menores. Para calcular la mediana, primero se deben ordenar los datos. Luego se determina el valor del dato que ocupa la posición central. Resulta apropiada cuando el conjunto de datos posee observaciones extremas.
Para un número impar de valores. La ubicación de la mediana de n datos ordenados corresponde al valor del dato ubicado en la posición (n +1)/2.
Cuando se tiene un número par de valores, la mediana corresponde al promedio aritmético de los dos valores en posición central.
Moda
Es el valor de un conjunto de datos que aparece con mayor frecuencia. Esta medida no depende de los valores extremos. Cuando no hay ningún valor con frecuencia mayor, la distribución carece de moda. También se puede dar el caso de una distribución con más de una moda. Es una medida “inestable” cuando el número de datos es reducido.
Rango medio
Es la media de las observaciones mayores y menor, pero si hay valores extremos, se distorsiona como medida de posición, pero frecuentemente ofrece un valor adecuado rápido y sencillo para resumir un conjunto de datos.