Prueba de Bartlett para homogeneidad de varianzas
Esta prueba considera el siguiente par de hipótesis.
Ho: Todas las varianzas son iguales
Ha: Al menos dos varianzas son diferentes
Consiste básicamente en obtener un estadístico de contraste cuya distribución se aproxima a una distribución ji-cuadrada, con a-1 grados de libertad, cuando las a muestras aleatorias son de poblaciones normales independientes. La secuencia de cálculo es:
1. Considerando la fórmula

4. Calcula
5. Obtener el valor calculado de ji-cuadrada y compararlo con el valor de tablas con nivel de significancia α y a-1 grados de libertad. Regla de decisión:
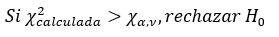
Prueba de Levene modificada
Debido a que la prueba de Bartlett es sensible al supuesto de normalidad, hay situaciones donde se recomienda un procedimiento alternativo, como lo es éste método robusto en cuanto a las desviaciones de la normalidad, ya que se basa en las medianas y no enlas medias de los tratamientos.La secuencia de cálculo es:
Primero y antes que nada considerar el par de hipótesis a trabajar.
Ho: σ12 = σ22 = σα2 Todas las varianzas son iguales
Ha: Al menos dos varianzas son diferentes
1. Obtener la mediana de cada tratamiento:
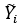
Obtener para cada dato del experimento el valor absoluto de la desviación de cada observación con respecto a la mediana de su tratamiento.

3. Sobre la tabla de estas diferencias, realizar un ANOVA y aplicar la regla de decisión sobre el estadístico F para rechazar o no la Hipótesis nula.
