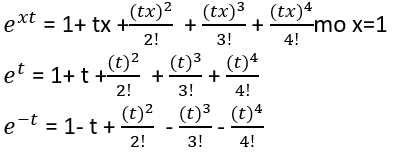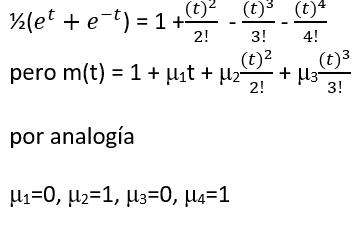Función de distribución
La función de distribución describe el comportamiento probabilístico de una variable aleatoria X asociada a un experimento aleatorio y se representa como:
F(x) ó Fx
Iniciemos con la pregunta:
¿Cuál es la probabilidad de que una variable aleatoria tenga un valor menor o igual a un número definido?
La respuesta se da por la función de distribución acumulativa FDA, definida como sigue:
Si X es una variable aleatoria y x es un número real, la función de distribución acumulativa de X, representada por F(x), que muestra la probabilidad de que x asuma valores menores o iguales a x es:

Una función de distribución acumulada que define inmediatamente de su función de probabilidad
Como puede observarse del experimento de lanzar 4 monedas y observar águilas:

Una Función de Distribución Acumulada debe satisfacer las siguientes necesidades:
1.- 0 ≤ F(x) =1
2.- F(a) ≤ F(b), si a < b. Esto implica que FDA es una función no decreciente y que P(a < X ≤ b) = F(b) – F(a)
3.- F(α) = P(X ≤ α) =1 y F(-α) = P(X ≤ -α) =0.
La función de distribución acumulada es:


Funciones de distribución continua
Sea X una v.a. que solo puede encontrarse en cierto intervalo finito para los números finitos a y b, se dice que tiene una distribución uniforme o rectangular; si su función de densidad de probabilidades es constante en el intervalo de a a b. Así para un modelo uniforme, la probabilidad de cualquier hecho que es un subintervalo de [a, b] es precisamente la razón (cociente); pero la probabilidad de un hecho que no tiene puntos comunes en [a, b] es cero, de modo que:

También puede demostrarse que:

Este modelo tiene a y b como parámetros y su esperanza y varianza son:

Ejemplo
Suponiendo que X tiene una distribución uniforme en el intervalo -1 ≤ x ≤ 1, encontrar f(x); y I(x), además calcular P(x >0), P(0 ≤ x ≤ 0.3) y P(x = 0.5)
Si X es una variable aleatoria continua, entonces la regla de la correspondencia que define la función distribución acumulada F(X) es:

Se ha usado v para representar la variable de integración, ya que X se usa para representar al límite superior de la integración. El integrando es la función densidad de probabilidad, y al derivar la expresión anterior (Teorema Fundamental del Calculo) se tiene que:
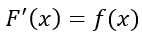
Función Generalizada de Momentos
Sea X una v.a. con función de densidad de probabilidad f(x). El valor esperado de ext está definida como la función generatriz de momentos de X, para cada t en el entorno –h < t < h; h > 0. La función generatriz de momento denotada por x(t) o m(t) es:

Si se supone que m(t) se puede desarrollar en pares de polinomios de t, convergente, se puede demostrar que:
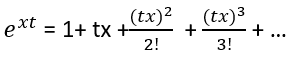
De modo que multiplicando por f(x) e integrando (aceptando que las integrales existen)

Donde μn es el coeficiente de tn /n! en el desarrollo de polinomios de m(t), y μ se define como el momento al 1er momento se le define como E(x).
Ejemplo
Sea X una v.a. que toma valores 1 y -1 con probabilidades de ½ c/u..
- Hallar la función generatriz del momento m(t) =e xt
a) si x toma valores 1 y -1 y f(x) = ½ se tiene:

b) Los primeros 4 momentos alrededor del origen: