Un concepto básico en el cálculo de probabilidades es el de Evento, ya que siempre que se habla de probabilidades se hace como Probabilidad de un Evento.
Ejemplos de Eventos:
A: Obtener águila en el lanzamiento de una moneda
B: Obtener un número par en el lanzamiento de un dado
C: Obtener un As al extraer una carta de una baraja.
Al hablar de la probabilidad de cada evento se pueden comparar en términos de la frecuencia con que se espera que ocurriera cada uno, en caso de que el experimento se repitiera un gran número de veces. En cualquier experimento aleatorio se pueden distinguir ciertos resultados que son los más simples de todos y se llaman elementales. Así, de cualquier evento puede definirse como una condición de resultados elementales.
Definición.
A un evento que consta de un solo resultado elemental se le llama Evento de Elementos.Cuando un evento está compuesto de resultados elementales, su probabilidad es igual a la suma de las probabilidades de los eventos elementales correspondientes.
Demostración.
El evento seguro está compuesto por todos los resultados elementales. Suponiendo que cada evento correspondiente tiene propiedad p. Entonces, la probabilidad del evento seguro, o sea 1, es igual a M veces la probabilidad, esto es: 1 = M•p de donde p = 1/M
Proposición 1.
Cualquier evento está compuesto por resultados elementales. Entonces, la probabilidad de dicho evento es igual a la suma de las probabilidades de los eventos elementales correspondientes.
Teorema 1.
Supóngase un experimento aleatorio con M eventos elementales equiparables. Entonces, laprobabilidad de cada uno de ellos es igual a 1/M.
Estas son las nociones Elementales de Conjuntos:
1)Sea S = espacio muestral, con S conjunto de todos los resultados elementales de un experimento aleatorio.
2)Un Evento es un conjunto de resultados elementales.
3)Un Evento Ocurre cuando ocurre alguno de los resultados elementales que lo componen.
4)El conjunto vacío es igual a aquel que no tiene resultado elemental alguno (Ø).
5)En terminología de eventos A U B es un evento que ocurre cuando al observar el resultado del experimento, puede decirse que ocurrió A, que ocurrió B y posiblemente los dos.
6)En el contexto de Eventos A ⋂ B es un evento que ocurre cuando el resultado del experimento indica A y B a la vez.
7)Una noción muy importante es la de Incompatibilidad entre conjuntos. Se dice que 2 conjuntos son mutuamente excluyentes si no existe ningún elemento que pertenezca simultáneamente a los dos conjuntos, en otras palabras cuando A⋂B = Ø
Elementos de La Teoría de Probabilidad
Condición: Experimentos Aleatorios donde el conjunto de resultados elementales es finito.
a) Para cualquier A, la probabilidad es no-negativa, esto es, P(A) ≥ 0
b) Si en un experimento aleatorio, S es el evento seguro, entonces P(S) = 1
c) La probabilidad de un evento A es igual a la suma de las probabilidades cuya unión es igual a A. De las condiciones anteriores, se deducen los siguientes resultados:
Teorema 2
Si A y B son eventos de un experimento aleatorio y además son mutuamente excluyentes, entonces:
P(A U B) = P(A) + P(B)
Teorema 2.1
Si A y B son eventos cualesquiera de un experimento aleatorio, entonces
P(A U B) = P(A) + P(B) –P(A ⋂ B)
Demostración
A U B = A U(B ⋂ Ac)
1° A U B
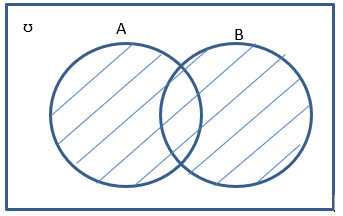
2° B ⋂ Ac
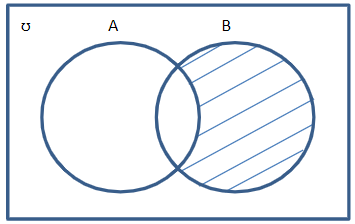
3° A U (B ⋂ Ac)
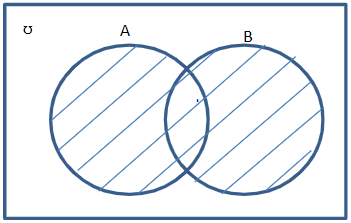
Luego entonces
P(A U B) = P(A) + P(B ⋂ Ac)
De 2° se puede ver que B= (B ⋂ Ac) U (A ⋂ B)
Como son eventos independientes
P(B) = P(B ⋂ Ac) + P(A ⋂ B)
Despejando P(B ⋂ Ac):
P(B ⋂ Ac) = P(B) -P(A ⋂ B) ∴
P(A U B) = P(A)+ P(B) -P(A ⋂ B)
Teorema 3
Si A es cualquier evento de un experimento aleatorio y Ac es su complemento, entonces
P(Ac) = 1 –P(A)
Demostración:
A U Ac= S ∴ P(A U Ac) = 1, 1 = P(A) + P(Ac)
despejando
P(Ac) = 1 –P(A)
Corolario
La probabilidad de un evento imposible es 0.
P(Ø) = 0
