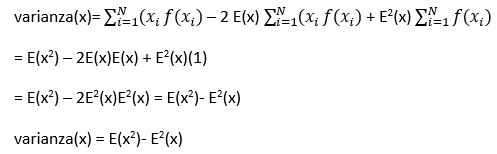Supóngase que en una clase de 50 alumnos se les aplica un examen de 5 preguntas, sea x el número de respuestas correctas por cada estudiante.
1.- ¿Qué valores puede tomar x?
x=0, 1, 2, 3, 4 o 5.
2.- ¿Cómo puede determinarse el promedio final del grupo?
Para esto, conociéndose los posibles resultados de la clase de 50.

Debido a las repeticiones de las observaciones, el promedio puede obtenerse como un promedio ponderado.
Promedio = 0(2/50) + 1((2/50) + 2(6/50) + 3(6/50) + 3(20/50) + 4(15/50) + 5(5/50)
Promedio = 3.18
Ahora supóngase que dicho examen le es aplicado a un gran número de estudiantes. Entonces, las observaciones pueden resumirse como:


Por analogía con el ejercicio anterior, el valor pomedio se puede encontrar como la media ponderada de los valores posibles de x, los cuales son ponderados por la probabilidad apropiada.
Este valor de x se llama la esperanza matemática de x, el valor esperado de x o la media de x, siendo simbolizada por E(x), μx o μ
¿Qué debe entenderse por esperanza matemática?
No se utiliza en el sentido ordinario de la palabra, este valor es “esperado” en el sentido de que supone experimentos repetidos una gran cantidad de veces los resultados se acercan mucho a este valor.
Definición
Sea X una variable aleatoria con una función de probabilidad

Entonces el valor esperado de X está dado por:
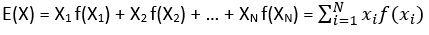
Ejemplo
Sea x una v.a con f.d.p.

El ejemplo anterior nos lleva a la siguiente definición:
Definición
Sea x una variable aleatoria con función de probabilidad

y H una función de X, esto es, H(x), entonces el valor esperado de la función H(x) es:
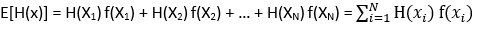
Leyes de la esperanza para una sola v.a.
Considerando a E como un operador lineal.
Teorema
Dada X una v.a. con f.d.p. f(xi) para i=1, 2, …, N y un valor medio E(x). Entonces E(ax+b) = aE(x)+b, donde a y b son constantes.
Demostración
Por definición:
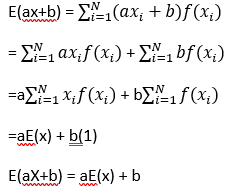
Considerando algunos casos especiales
- Si a=0, entonces tenemos
a) E(b) = b;
esto es el valor esperado de una constante, es la constante misma.
b) Si b=0, entonces
E(ax) = aE(x),
esto dice que si cada valor de una variable aleatoria se multiplica por una misma constante “a”, entonces, la media de la distribución de ax de “a” veces la media de x.
c) Si a=1, entonces
E(ax+b) = E(x) +b
d) E(X-M) =0, esto se obtiene directamente del teorema con a=1 y b=-M
E(X-M) = E(X)-M dado que E(X)=M
E(X-M) =0
El valor esperado de la desviación de cualquier v.a, con respecto a su media es cero.
Varianza
Dadas las siguientes gráficas.

a) ¿Cuál es el valor de E(X), E(Y) y E(Z)?
b) ¿Son o no son idénticas las 3 f.d.p´s.?
c) ¿Si son diferentes como podría medir su diferencia?
En realidad hay varias formas de medir dicha diferencia pero nos enfocaremos a cuantificar la amplitud o variabilidad con respecto a la media. Nosotros podemos esperar que dicha medida sea más pequeña cuando la distribución es más compacta alrededor de la media y más grande cuando la distribución está más dispersa. De tal forma que nos enfocaremos a cuantificarla por medio de “Desviaciones cuadradas con respecto a la media” y le llamaremos “Varianza” a dicho valor.
Sea Z una v.a. con f.d.p. f(xi) para i=1,2, … , N y media E(X) =M. Entonces la varianza de x, var(X), está definida por:
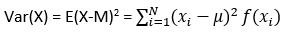
Nótese:
- que este es un caso especial de H(X), cuando f(X) = (X-μ)2,
- la varianza también es denotada por σ2
- Que la medida utilizada es una función de desviaciones cuadradas con respecto a la media, siendo útil tener una medida en unidades originales de tal forma que tomaremos la raíz cuadrada positiva de la varianza. Esto se definirá a continuación
Desviación estándar
La desviación estándar de X es la raíz cuadrada positiva de la varianza, la cual está dada por
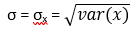
Teorema
Una fórmula fácil de manejo para el cálculo de la varianza es:
Var(x) = E(x2) – [E(x)]2
Demostración:
Var(x) = E(x2) – [E(x)]2
Por definición:

como E(x) = μ ó μ =E(x)

Aplicando propiedades de la sumatoria: