Si se cumplen los supuestos de que los datos distribuyen normalmente con media cero, varianzas iguales y las variables son independientes, entonces se aplica una prueba de “t” para comprobar si a y b son diferentes de 0 , si es diferente entonces el modelo se desecha.Cada variable tiene una distribución t de Student con n-2 grados de libertad, lo que permite efectuar pruebas de hipótesis y calcular intervalos de confianza sobre los parámetros de regresión β0 y β1 .
Un caso de particular interés es probar la hipótesis:
Ho: β1=0
H1: β1 ≠0
Ya que si la pendiente es igual cero, entonces puede significar o que la variación de X no influye en la variación de Y, o que no hay regresión lineal entre X y Y.
Por otro lado, si la pendiente es diferente de cero, entonces existirá algún grado de asociación lineal entre las dos variables, es decir, la variabilidad de X explica en cierta forma la variabilidad de Y (aunque no implica que no pueda obtenerse un mejor ajuste con algún polinomio de mayor grado en X).
La correlación determina el grado de asociación entre las dos variables, en otras palabras, explica el impacto que tiene el cambio de una variable en el cambio de la otra. La correlación sigue los siguientes supuestos:
X y Y son variables aleatorias, por lo que designarlas como dependiente e independiente dará el mismo resultado.
La población bivariada es normal.
La relación entre X y Y es lineal.
Correlación
grado de asociación entre las 2 variables, está determinado por el coeficiente de correlación.
r = el grado de asociación y se calcula con la fórmula:
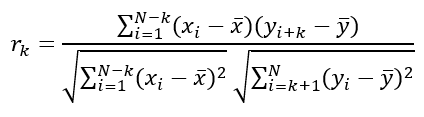
Tipos de correlación

