Diagrama de Cajas y Bigotes (Box-plot)
El diagrama de caja es una presentación visual que describe al mismo tiempo varias características importantes de un conjunto de datos, tales como el centro, la dispersión, la simetría o asimetría y la identificación de observaciones atípicas (una observación que parece desviarse notablemente de las otras observaciones de la muestra en la que aparece). El diagrama de caja representa los tres cuartiles, y los valores mínimo y máximo de los datos sobre un rectángulo (caja), alineado horizontal o verticalmente.
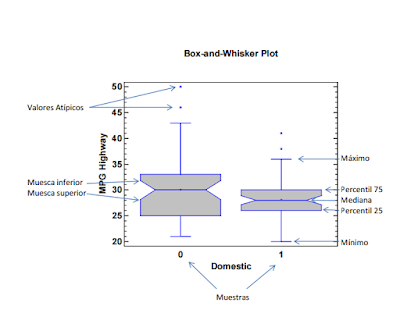
Nota: Los percentiles de un conjunto de observaciones dividen en centésimos la frecuencia total. Esto es, el p-percentil o el percentil p es el valor por debajo del cual se presenta el p% de las observaciones. Así, el percentil 50 es el valor por debajo del cual se tiene el 50% de las observaciones.
A veces se necesitan valores que dividen el porcentaje total en partes iguales como: cuartos, décimos, quintos o tercios. Los puntos de división para estas distintas particiones se llaman cuartiles, deciles, quintiles y terciles, respectivamente. Así, el primer cuartil corresponde al percentil 25, ya que es el primer cuarto. El séptimo decil equivale al percentil 70, el segundo cuartil o el quinto decil son otras formas de llamar al percentil 50 (Marques, 2004).
Construcción de un diagrama de cajas y bigotes
- Ordenar los datos de menor a mayor.
- Calcular la mediana, el cuartil inferior, el cuartil superior y la distancia intercuartil (DI, RQ, DC)
- Calcular las cotas que permitán decidir si un dato es outlier (atípico):
– 2ª cota inferior = CI – 3 DI- 1ª cota inferior = CI – 1.5 DI- 1ª cota superior = CS + 1.5 DI- 2ª cota superior = CS + 3 DICualquier dato que “caiga” entre la 1ª y 2ª cota inferior o entre la 1ª y 2ª cota superior será declarado outlier. Cualquier dato que caiga por fuera de la 2ª cota inferior o la 2ª cota superior será declarado outlier severo.
- Dibujar una escala que cubra el rango de variación de los datos y marcar la mediana y los cuartiles. Dibujar una caja que se extienda entre los cuartiles y marcar en ella la posición de la mediana.
- Partiendo del cuartil inferior trazar una línea (bigote) que llegue hasta el último dato contenido “dentro” de la 1ª cota inferior.
Partiendo del cuartil superior trazar una línea (bigote) que llegue hasta el último dato contenido “dentro” de la 1ª cota superior.
- Marcar la posición de los outliers con un símbolo (por ejemplo, *) y de los outliers severos con otro símbolo (por ejemplo, ○).
GRÁFICOS
El objetivo de un gráfico es apreciar, de manera visual, los datos como un todo e identificar sus características sobresalientes. La selección de un gráfico depende del tipo de variable que se quiera representar, por esta razón se hace revisan tanto gráficos para variables categóricas como para variables numéricas.
Diagrama de Tallo y Hoja
Para representar un conjunto de datos cada valor numérico se divide en dos partes. El o los dígitos principales forman el tallo y los dígitos secundarios las hojas. Los tallos se colocan en el eje vertical y las hojas de cada observación en el eje horizontal.Pasos para hacer un Tallo y Hoja
1. Separar cada medida en un tallo y una hoja. Generalmente la hoja consiste en exactamente un dígito (el último) y el tallo consiste en uno o más dígitos.
Ejemplos:
734 => tallo=73, hoja=4; 2) 4,345 => tallo=434, hoja=5.
Es importante añadir, en un diagrama de tallo y hoja, la indicación de cómo están representados los datos (si los valores del tallo son unidades o decimales, etc.)
Para 4,345, por ejemplo, se puede decir que 434 | 5 se debe leer como 4,345.
2. Escribir los tallos en orden creciente de arriba abajo y dibujar una línea a la derecha de los tallos.
3. Agregar las hojas a su respectivo tallo en orden creciente.
Ejemplo 1
Conjunto de datos, en cm: 11,357; 12,542; 11,384; 12,431; 14,212: 15,213; 13,300; 11,300; 17,206; 12,710;13,455; 16,143; 12,162; 12,721; 13,420; 14,6982. Datos redondeados expresados en mm:114; 125; 114; 124; 142; 152; 133; 113; 172; 127; 135; 161; 122, 127; 134; 1473. Diagrama de tallo y hojas, datos en mm:
11 | 2 representa 11211 | 4 4 312 | 5 4 7 2 713 | 3 5 414 | 2 715 | 216 | 117 | 2
Cuando el primer dígito de la clasificación varía poco, la mayoría de los datos tienden agruparse alrededor de un tallo y el diagrama resultante tiene poco detalle. En ese caso es conveniente subdividir cada tallo en dos o más partes introduciendo algún signo arbitrario (usualmente se utiliza * para agrupar los dígitos del 0 al 4 y • para los datos del 5 al 9), como se indica:
Ejemplo 2.
Las pulsaciones por minuto de un grupo de 40 ratones se representan en el siguiente diagrama de tallo y hojas.
5 | 2 66 | 0 0 0 0 0 0 4 4 4 4 4 4 8 8 8 8 8 8 8 87 | 2 2 2 2 2 2 2 2 6 6 6 6 68 | 0 0 4 4 8 89 | 2
Se puede obtener más detalle subdividiendo cada tallo en dos partes iguales: en una se colocan las hojas 0 a 4 y se representa ( * ), en la otra parte se ubican las hojas de 5 a 9 y se representa por (•), obteniendo el diagrama:1ǀ2 representa 12
5 * 25 • 66 * 0 0 0 0 0 0 4 4 4 4 4 46 • 8 8 8 8 8 8 8 87 * 2 2 2 2 2 2 2 27 • 6 6 6 6 68 * 0 0 4 48 • 8 89 * 2
Otra opción es la de Cinco ramas por tallo. Consiste en subdividir cada tallo en 5, cada uno de las cuales incluirá dos posibles valores para el primer dígito de cada hoja, en este caso se añaden las letras de los números en inglés:
- En * se colocan 0 y 1.
- En “t” (two, three) se colocan 2 y 3.
- En “f” (four five) se colocan 4 y 5.
- En “s” (six, seven) se colocan 6 y 7.
- En • se colocan 8 y 9.
