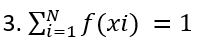Definición
Una variable cuyos valores numéricos quedan determinados por los resultados de un experimento se llama VARIABLE ALEATORIA. Así la variable x que representa el número de caras obtenidas al lanzar 3 monedas es una variable aleatoria.
NOTA: Es conveniente distinguir entre la variable aleatoria y los valores numéricos que ella puede tomar, para esto se designa a X (mayúscula) como la variable aleatoria y a x (minúscula) como los valores que puede tomar.
Las variables aleatorias se clasifican en discretas y continuas:
Discreta
La variable aleatoria X se dice que es discreta si los números asignados a los sucesos elementales de E sólo toman valores enteros. Sus posibles valores constituyen un conjunto finito o infinito numerable. Por ejemplo, supongamos el experimento consistente en lanzar tres veces una moneda no trucada; si consideramos la variable aleatoria X=número de caras obtenidas en los tres lanzamientos, los valores que puede tomar esta variable aleatoria son finitos (0,1,2,3).
Continua
La variable aleatoria X será continua si los valores asignados pueden ser cualesquiera, dentro de ciertos intervalos, es decir, puede tomar cualquier valor de R. Por ejemplo, si consideramos el experimento aleatorio consistente en medir el nivel de agua en un embalse y tomamos la variable aleatoria X= nivel de agua, esta puede tomar valores entre 0 y más infinito, considerando todos los valores decimales dentro de estos.
Para definir una variable aleatoria y sus funciones de probabilidad, para esto considérese el experimento de lanzar 3 monedas honestas, todos los resultados posibles son:
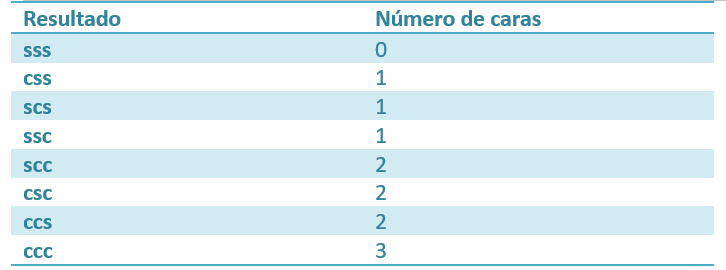
Se ha asignado un valor numérico (0,1,2 o 3) a cada uno de los resultados posibles.
Sea el evento x: obtener una cara
A x se le asigna un valor 1,2,3 o 3 según sea el resultado del experimento.
Ejemplo.
Experimento: Observar al azar a dos niños recién nacidos.
Suponiendo que nos interesa el evento x: número de varones; el espacio es:

De aquí que X puede tomar 3 valores x1=0, x2=1 y x3=2
Algo que es importante notar es:
UN VALOR DE UNA VARIABLE ALEATORIA, TIENE UNA PROBABILIDAD.
Así si X es una variable aleatoria que puede asumir valores x1, x2…. xn con probabilidades asociadas p1, p2, … , pn, entonces el conjunto de pares ordenados (xi,pi); c=1,2, …, n se llama función de probabilidad, definida por la forma:
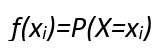
Para el ejemplo de los niños se tiene:

Una función de una variable aleatoria discreta X, donde X asume N valores x1, x2…. xN, es una función de probabilidad, si y solo si, satisface los 3 requisitos siguientes:
- La función f(xi) asume un valor numérico para todas las xi, 1≤i≤N
- f(xi)> 0 para cualquiera de los valores posibles de X