Para obtener la gráfica del polinomio
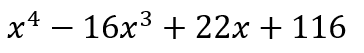
empezaremos por utilizar el comando linspace
Este comando genera un vector con N puntos igualmente espaciados a partir de un valor de x mínimo y uno máximo; es decir, permite manejar un rango de puntos que mejor ajuste al polinomio en el eje x. Por ejemplo, linspace (– 2, 3, 10) produce diez datos equidistantes entre – 2 y 3.
Si no se especifica el último dato, como en
x = linspace ( – 2, 3 );
se produce un vector de 100 entradas con la primera igual a – 2 y la última igual a 3
Ahora, se efectúa la designación del polinomio
>> p = [ 1 –16 0 22 116];
Después, se evalúa el polinomio p(x) en x y el resultado es almacenado en y con el comando polyval
>> y = polyval ( p , x );
Para obtener la gráfica del polinomio anterior, es necesario utilizar la función plot, esta función traza una curva al unir los puntos x(i), y(i) en secuencia y de manera automática. Esta función se escribe en MATLAB de la forma:
>> plot (x , y)
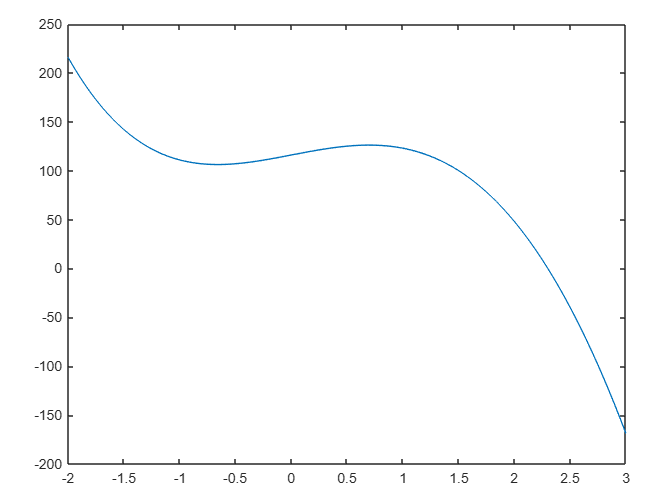
La orden plot abre la ventana gráfica, llamada ventana de figura, escala los ejes para ajustar los datos, representa los puntos y a continuación conecta los puntos con una línea recta. También añade una escala numérica y coloca de forma automática marcas en ambos ejes. Observa la gráfica o figura que se va generando con los comandos siguientes.
title ( ‘ x ^4 – 16 x^3 + 22x +116 ‘ )
La función title permite colocar un título a la gráfica. Aquí el texto entre paréntesis y comillas es lo que se despliega. Ahora se complementan los datos con las etiquetas en los ejes con el comando xlabel (‘ x’‘) y, ylabel (‘ y’)
xlabel (‘ Eje x ‘)
ylabel (‘ Eje y ‘)
Se muestra incluso la rejilla con el comando grid.
grid on
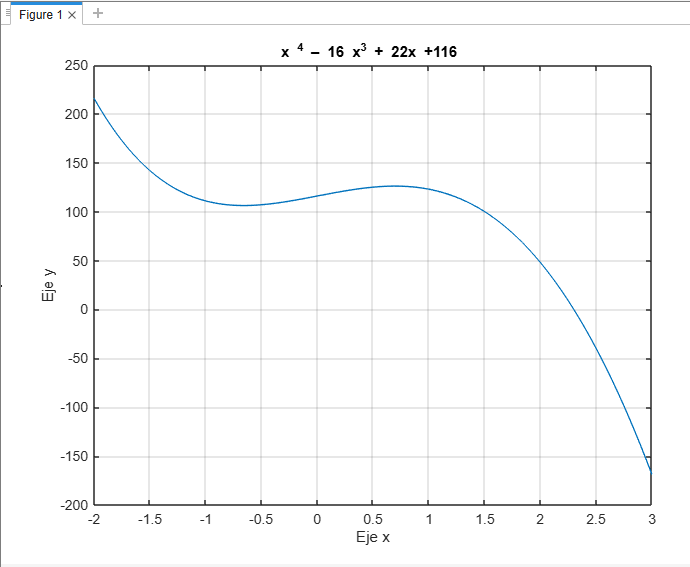
Al observar el grado del polinomio se aprecia que es de cuarto orden, y que por consiguiente tiene cuatro raíces que se obtienen con la función roots.

Hay dos raíces reales y dos complejas. Una de las raíces reales se pueden apreciar en el gráfico cuando la curva pasa por la línea en donde y = 0.
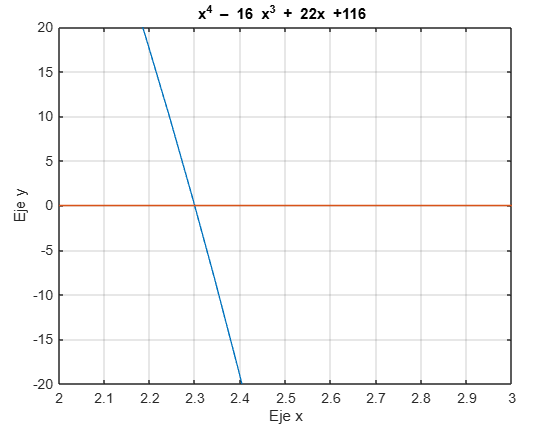
En la gráfica la raíz 2.2995 es la que se muestra en la intersección entre 2.2 y 2.4.
Reto. Para observar la otra raíz real se debe cambiar el rango de x modificándolo por x = linspace(–2, 20) y repitiendo las líneas anteriores. El resultado debe ser similar al mostrado en la siguiente figura.
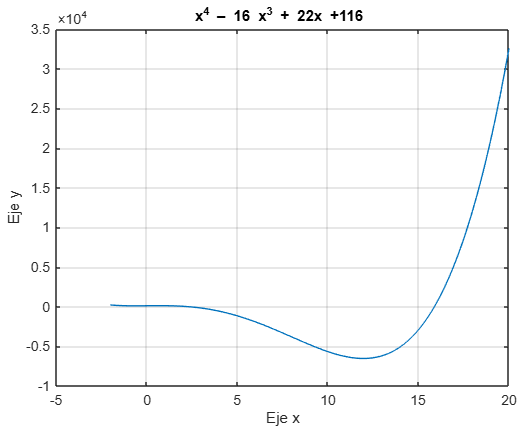
Para cambiar el área de visualización se utiliza el comando axis en la forma axis([x1 x2 y1 y2]).
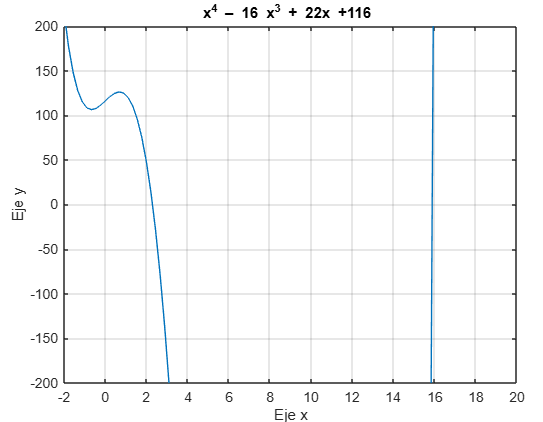
Prueba con axis ([–2 20 –200 200]) en la ventana de comandos y observa el cambio en la figura. Se aprecian las dos raíces reales.
Trazos de funciones sobre la misma gráfica
Cada vez que se llama al comando plot, se abre una ventana para mostrar la figura, plot borra la ventana de la figura actual y dibuja una nueva gráfica. Ahora probar lo siguiente:
>> x = linspace (0,2*pi,30);
>> y = sin (x);
>> plot (x,y)
Este ejemplo, la instrucción linspace, crea 30 datos en el intervalo 0 ≤ x ≤ 2π para formar el eje horizontal del gráfico y crea otro vector que contiene la función seno de los datos almacenados en x. La gráfica se aprecia en la siguiente figura.
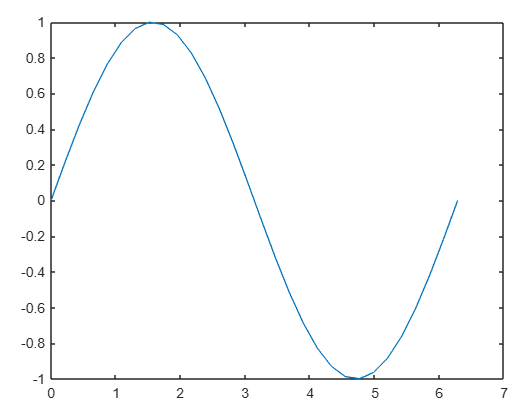
Ahora se representará la función seno con la función coseno sobre la misma gráfica con las instrucciones
>> z = cos (x);
>> plot (x, y, x, z)
>> grid on
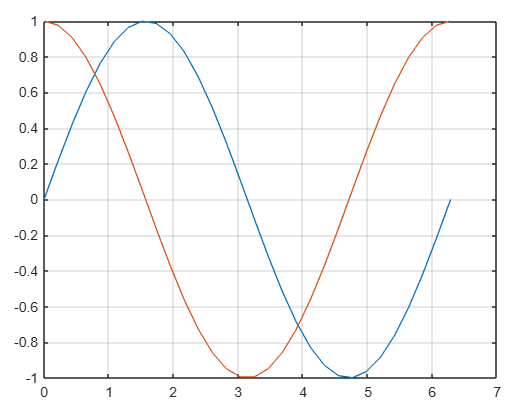
Este ejemplo muestra que se puede representar más de un conjunto de escalares al mismo tiempo, simplemente dando a plot otro par de argumentos y automáticamente dibujará la segunda curva en un color diferente sobre la figura.
De esta forma se pueden representar al mismo tiempo muchas curvas suministrando parejas adicionales de argumentos a plot. Otra forma es utilizar la instrucción hold on que permite ingresar varias graficas con varios plot(x,y). Para desactivar se emplea hold off.
Estilo de líneas, marcadores y colores
Se puede especificar el tipo de color y estilo de línea para las gráficas según se desee escribiendo un argumento adicional en el comando plot. Los elementos adicionales son
| Símbolo | Color | Símbolo | Estilo de línea |
| y | amarillo | . | punto |
| m | magenta | o | círculo |
| c | azul | x | cruces |
| r | rojo | + | más |
| g | verde | * | estrella |
| b | azul | – | línea sólida |
| w | blanco | : | línea punteada |
| k | negro | – . | línea punto |
La forma como se insertan es después de cada par de datos como se indica en las siguientes líneas
x= linspace(0,5); y= sin(x); z= cos(x); plot(x,y,'b+',x,z,'g*')
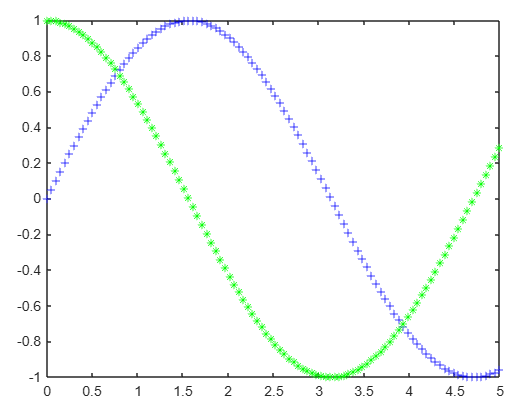
Escalas de los gráficos 2-D
Se pueden utilizar otras escalas logarítmicas o semi logarítmicas para representar los datos tanto en el eje X como en el eje Y al sustituir el comando plot por otro.
♦ Escalas logarítmicas en ambos ejes.
loglog (x, y)
♦ Escala logarítmicas en el eje X y escala lineal en el eje Y.
semilogx (x, y)
♦ Escala logarítmica en el eje Y con escala lineal en el eje X.
semilogy (x,y)
Aplicando la opción loglog (x, y) a los datos de x = linspace(0.1,3), con la función y = sin(x), se obtiene la siguiente gráfica con grid on.
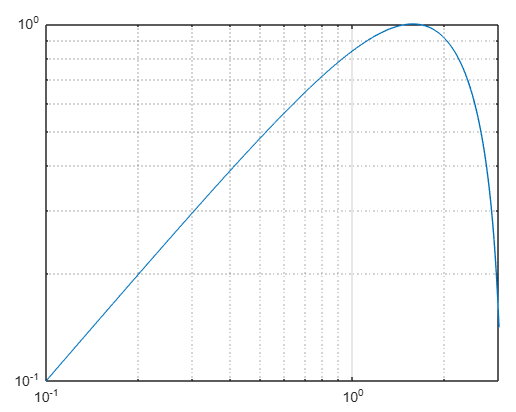
Las otras escalas dan las siguientes figuras
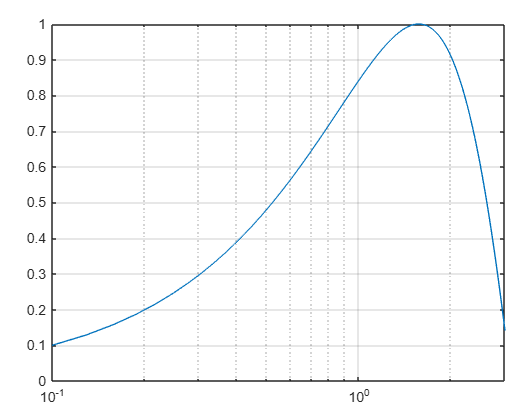
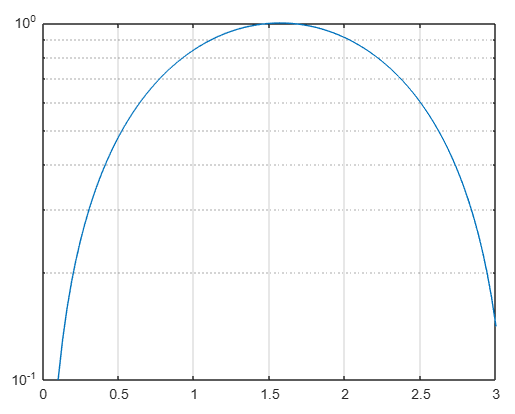
Tarea 3

Para el primer ejercicio utilice un rango de 0 a 5, y para el segundo de 0 a 25.