Sistema de ecuaciones lineales 

La información dada en la sección anterior tiene su mayor aplicación
en la solución de un sistema de ecuaciones lineales. Estas ecuaciones
se pueden organizar en una ecuación matricial donde la manipulación
se puede realizar a través de funciones predefinidas de Matlab o a
través de instrucciones secuenciales. Sea el sistema de tres ecuaciones
con tres incógnitas ( x, y, x ) donde el sistema queda establecido
así.

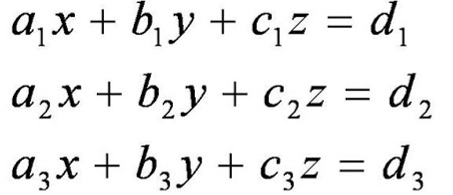
Ordenando en forma matricial se tiene

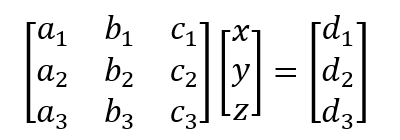
Ahora asignando a cada arreglo un vector y matriz según corresponda,
se tiene A X = d

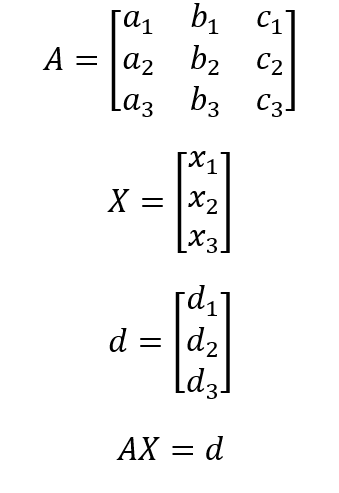
Donde A es la matriz coeficiente del sistema, X es el vector incógnita y
d el vector de términos independientes.

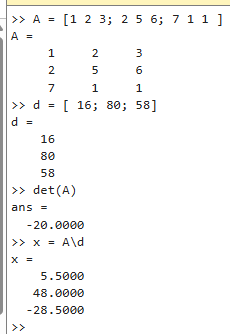
Primero el programa MATLAB tiene que conocer la matriz de coeficientes de la ecuación.
>> A = [1 2 3; 2 5 6; 7 1 1 ]
Luego, el vector del lado derecho. d = [ 16; 80; 58]
Este problema tendrá una respuesta siempre que el determinante de A sea distinto de cero. Para obtener el determinante de la matriz A, solo se tendrá que escribir en MATLAB el comando det(matriz)
>> det(A)
ans =
-20
Ahora que MATLAB tiene toda la información necesaria, ya se puede resolver el sistema de ecuaciones con la instrucción x = A \ d
El resultado es
>> x = A \ d
x =
5.5000
48.0000
– 28.5000
La respuesta de x interpreta los tres valores de las incógnitas x1, x2 y x3 en forma ordenada:
x(1) = 5.5 x(2) = 48 x(3) = – 28.5

Otra forma es utilizar la matriz aumentada y resolver con la función rref(A1). Esto es,

Tarea 4

Resuelva los siguientes sistemas de ecuaciones

a)	5x + 5y = 0 3x + 2y = – 2	x = – 2 y = 2
b)	2x + 3y + 2z = 6 4x + y + 4z = 2 3x + 6y + 2z = 14	x = 2 y = 2 z = – 2
c)	3x – y + z = 1 3x + 6y + 2z = 0 3x + 3y + 7z = 4	x = 0.0351 y = – 0.2368 z = 0.6579
d)	2(2x + 8) – 3y = 27 x + 2y – 1/3(3x – 2) = 5/3	x = 3.375 y = 0.833
e)	x + 2y = 3z + 4 5y + 5x = 4z – 6 6x + 2y = 5z + 2	x = – 1.7333 y = – 2.1333 z = – 3.333
f)	2x – 6y + 2 = -44 – 3x – y + 7z = -34 -8x + y – 2z = -20	x = 4 y = 8 z = – 2