La regla del trapecio es uno de los métodos más utilizados para calcular aproximaciones numéricas de integrales definidas. Es la primera de las fórmulas cerradas de integración de Newton – Cotes para el caso cuando el polinomio interpolante es de grado uno.
El nombre regla del trapecio se debe a la interpretación geométrica que se hace de la fórmula. Cuando el polinomio interpolante es de grado uno, su gráfica representa una línea recta en el intervalo [a, b] que es el área del trapecio que se forma, como se muestra en la figura.

Luego se tiene que la regla del trapecio viene dada por la fórmula:
A=∫f(x)dx ≈ 0.5(b−a)[f(a)+f(b)]
que aplica para un trapecio en el intervalo de la función.
Ejemplo 1. Calcular la integral de f(x) = x^3 – 6x + 3 en el intervalo [2, 5]
Solución. Se evalúa la función en f(2) y f(5) y aplicando la fórmula se obtiene una aproximación a la integral por medio de la fórmula del trapecio.
A = 0.5(5-2)[8-12+3 + 125-30+3] = 1.5(97) = 145.5
La solución analítica es
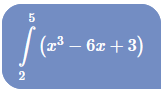
= 98.25
La grafica es la siguiente
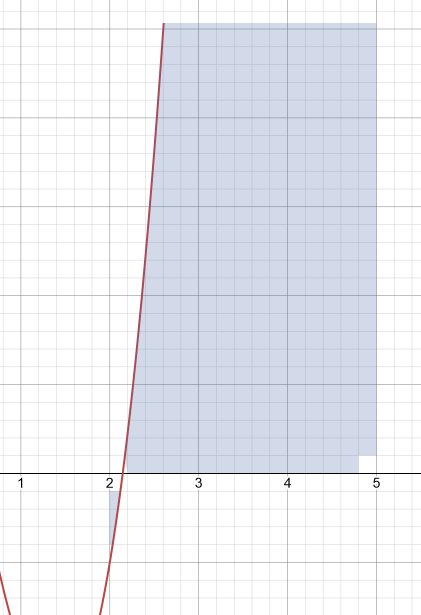
El error es muy grande, error = (98.25 – 145.5)/98.25 = 48.%; por lo que se recomienda utilizar varios trapecios para minimizar el error.
| x | f(x) |
| 2 | -1 |
| 3 | 12 |
| 4 | 43 |
| 5 | 98 |
Con tamaño de paso = 1 se forman 3 trapecios. La fórmula ahora se evalúa con los puntos conocidos.
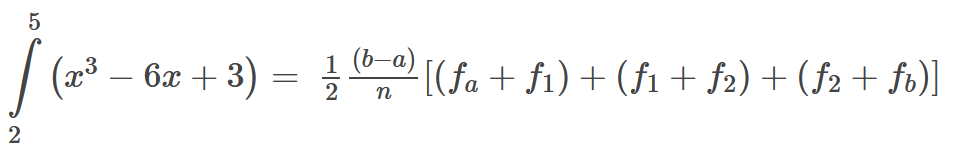
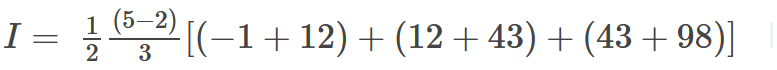
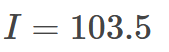
El error se reduce notablemente. error = 5.34 %
Utilizando un tamaño de paso de 0.5 la aproximación mejora bastante con 6 trapecios.
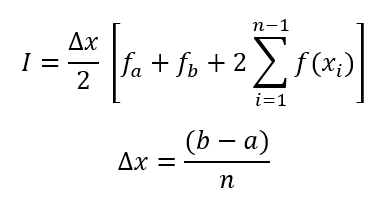
Programando en matlab
% Trapecio Integrales
fx=inline('x.^3-6*x+3')
a=2
b=5
fa=fx(a)
fb=fx(b)
% cambio de paso
n=6
dx=(b-a)/n
x=a:dx:b
y=fx(x)
I = 0.5*dx*(2*sum(y)-fa-fb)
error=abs(98.25-I)/98.25*100