El polinomio de Lagrange se genera con los datos tabulados y varios coeficientes. El polinomio de primer orden requiere dos puntos.
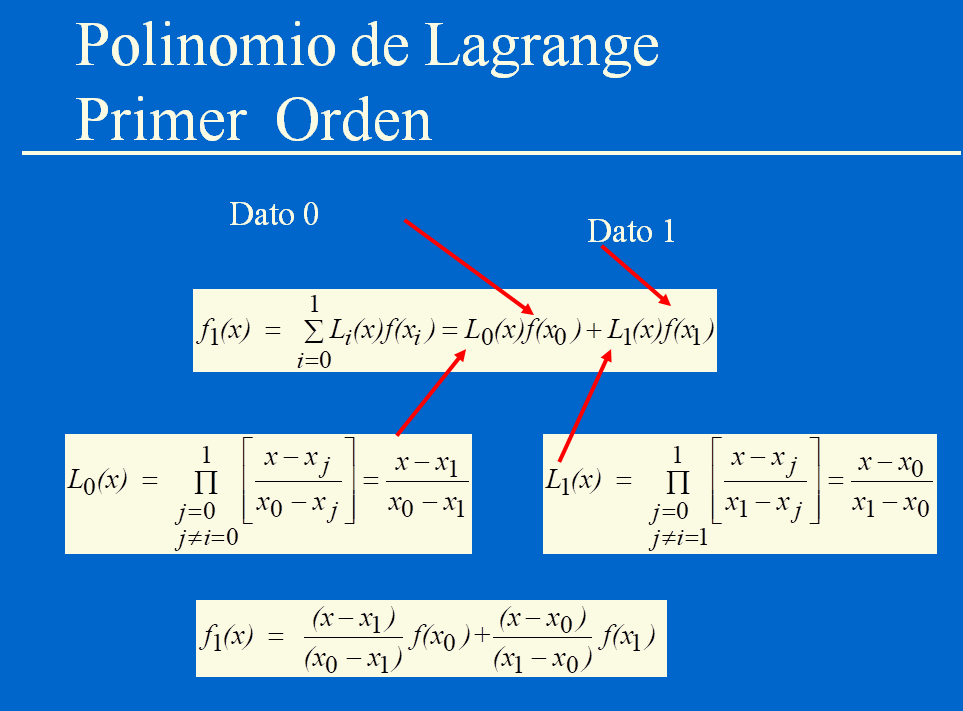
Para los datos
| x | 1 | 2 | 3 | 4 | 5 |
| y | 8 | 15 | 22 | 30 | 38 |
Primer orden
El polinomio de ajuste entre 2 y 4 se calcula como
x0 = 2 dato 0 = 15, x1 = 4 dato 1 = 30 L0 = (x - x1)/(x0 - x1) = (x - 4)/(2 - 4) = -0.5x + 2 L1 = (x - x0)/(x1 - x0) = (x - 2)/(4 - 2) = 0.5x - 1 f(x) = (-0.5x + 2)(15) + (0.5x - 1)(30) = 7.5x
| x | 2 | 3 | 4 |
| f(x) = 7.5x | 15 | 22.5 | 30 |
Segundo orden

Para los mismo puntos, esto es, 2 a 4.
x0 = 2 dato 0 = 15, x1 = 3 dato 1 = 22, x2 = 4 dato 2 = 30
L0 = (x-x1)(x-x2)/(x0-x1)(x0-x2) = (x-3)(x-4)/(2-3)(2-4) = 0.5x^2-3.5x+6
L1 = (x-x0)(x-x2)/(x1-x0)(x1-x2) = (x-2)(x-4)/(3-2)(3-4) = -x^2+6x-8
L2 = (x-x0)(x-x1)/(x2-x0)(x2-x1) = (x-2)(x-3)/(4-2)(4-3) = 0.5x^2-2.5x+3
f(x) = (0.5x^2-3.5x+6)(15) + (-x^2+6x-8)(22) + (0.5x^2-2.5x+3)(30)
= 0.5x^2 +4.5x + 4
Ejemplo
