El método de Zamora consiste en ordenar las ecuaciones de tal forma que cada uno de los elementos en diagonal sean unos, y por debajo de ellos sólo haya ceros.
Para el sistema
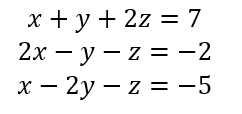
La matriz aumentada queda como
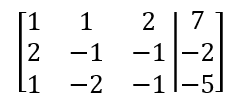
Primero hay que dividir R1 por 2 para hacer que el coeficiente en Z sea uno.
R1 = 0.5 0.5 1 3.5
Con este nuevo renglón 1 se hacen cero en la variable Z en los otros renglones,
R2 = R2 + R1 y R3 = R3 + R1
R2 = 2.5 -0.5 0 1.5 y R3 = 1.5 -1.5 0 -1.5
El nuevo sistema es ahora
- 0.5 0.5 1 3.5
- 2.5 -0.5 0 1.5
- 1.5 -1.5 0 -1.5
Ahora se hace uno el coeficiente de Y en el segundo renglón.
R2 = R2*(-2) = -5 1 0 -3
Después se elimina Y en el tercer renglón con R2
R3 = R3 + 1.5R2 = [1.5 -1.5 0 -1.5 ] + [-7.5 1.5 0 -4.5] = [-6.0 0 0 – 6.0]
El nuevo sistema es ahora
- 0.5 0.5 1 3.5
- -5 1 0 -3.0
- -6 0 0 -6
Haciendo uno en la variable X de la tercera ecuación, se encuentra que X = -6 /-6 = 1
sustituyendo en R2 Y = -3 + 5X = -3 + 5(1) = 2
sustituyendo en R1 Z = 3.5 – 0.5Y – 0.5X = 3.5 – 0.5(2) – 0.5(1) = 3.5 -1 – 0.5 = 2
La solución del sistema es X = 1, Y = 2, Z = 2
El método tiene la ventaja de disminuir la presencia de divisiones entre cero que ocurre en el método de Gauss, y no confundir el cálculo de las variables ya que primero se conoce X y al final la última variable, Z.
Código de programación
% GAUSS ZAMORA clc; R=[1 1 2 7;2 -1 -1 -2;1 -2 -1 -5] R1=R(1,:) R2=R(2,:) R3=R(3,:) % Hacer pivote 1 R1 R1=R1/R1(1,3) % Eliminación de Z en las dos ecuaciones siguientes R2=R2-R1*R2(1,3) R3=R3-R1*R3(1,3) % Hacer pivote 2 R2 R2=R2/R2(1,2) % Eliminación de Y en la ecuación siguiente R3=R3-R2*R3(1,2) % Solución x=R3(1,4)/R3(1,1) y=R2(1,4)-R2(1,1)*x z=R1(1,4)-R1(1,2)*y-R1(1,1)*x