Solución a ecuaciones no lineales
2.1 Raíces de una ecuación.
2.2 Bisección.
2.3 Newton-Raphson.
2.4 Secante.
2.5 Regla falsa.
2.6 Punto Fijo.
2.7 Müller.
La Ecuación es una igualdad entre dos expresiones
y = 2x + 5
A la variable independiente se le denomina dominio y a la variable dependiente se le dice rango. En el ejemplo, x es la variable independiente; y es la variable dependiente.
Para un dominio de x de [-3, 5], el rango para y es [-1, 15], su gráfica o imagen se ve así.
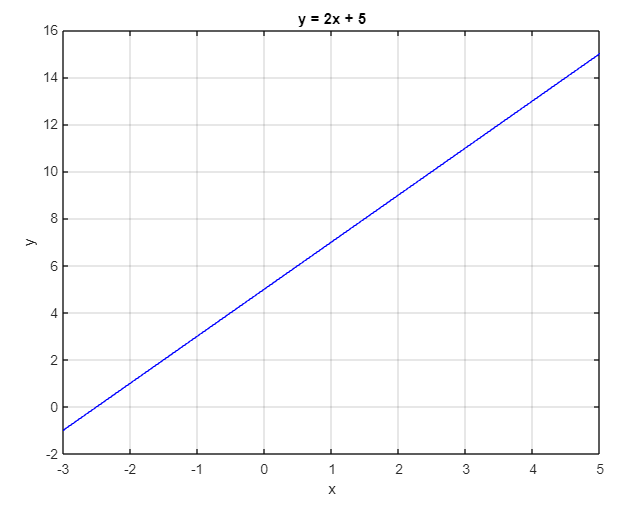
Cuando a cada elemento del dominio le corresponde solo un valor de la imagen, se dice que existe una función entre las variables (x, y), tal que y = f(x)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -1 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
Una función lineal se expresa como y = a + bx, donde a es la ordenada al origen cuando x = 0; y b es la pendiente de la recta. Para el ejemplo y = 2x+5, b = 2x, a = 5. Si b es positivo la pendiente es creciente. Esto es, conforme aumenta x el valor de y también aumenta. Si b es negativo entonces la función es decreciente.
Cuando b = 0 la función es una función constante.
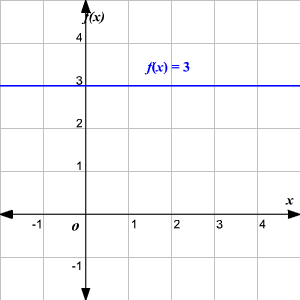
Cuando la función no es de la forma lineal, se le llama ecuación no lineal y se emplean métodos de solución que se describen en esta unidad.