El método más conocido para resolver sistemas de ecuaciones lineales es la “eliminación de Gauss”, que funciona eliminando variables de las ecuaciones al convertir en cero a los elementos que se encuentran por debajo de la diagonal principal.
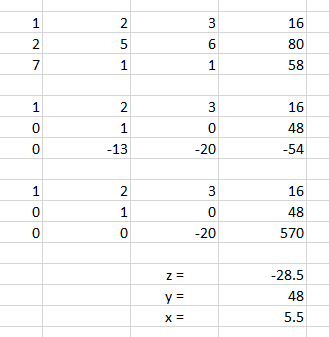
Las operaciones elementales que se utilizan en la eliminación de Gauss se pueden interpretar como operaciones de filas en la matriz aumentada. Estas consisten en:
- Permutar dos filas (intercambio de fila)
- Multiplicar una fila por un número diferente de cero, (R1 = 2*R1)
- Sumar un múltiplo de un escalar a otro renglón, (R2 = R2 + 2R1)
A continuación se resuelve con ayuda de MATLAB el siguiente sistema de ecuaciones por eliminación de Gauss.
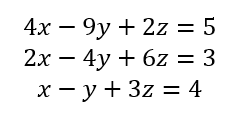
r1=[4 -9 2 5] r2=[2 -4 6 3] r3=[1 -1 3 4] r2 = r2 - r1/2 r3 = r3 - r1/4 r3 = r3 - 1.25/0.5*r2 z=1.5/-10 y=(2.75-2.5*z)/1.25 x=(5 - 2*z +9*y)/4
La solución del sistema es: x = 6.95, y = 2.5, Z = -0.15
Procedimiento
Dado que la primera entrada de la matriz es igual a 4, el primer paso es transformar en cero todas las entradas de la primera columna debajo del número cuatro.
R1 = [4 -9 2 5] R2 = R2 - R1/2 = [2 -4 6 3] - [2 -9/2 1 5/2] = [0 0.5 5 0.5] R3 = R3 - R1/4 = [1 -1 3 4] - [1 -9/4 1/2 5/4] = [0 1.25 2.5 2.75]
El sistema de ecuaciones resultante luego de eliminar x, es el siguiente:
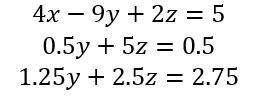
Ahora con el segundo renglón se debe eliminar “y” del tercer renglón
r3 = r3 - 1.25/0.5r2 R3 = [1.25 2.5 2.75] - 2.5[0.5 5 0.5] = [0 -10 1.5]
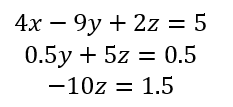
Sustitución hacia atrás
A partir de este sistema escalonado de ecuaciones se comienza a determinar el valor de cada variable, iniciando con la última ecuación.
z = - 1.5/10 = -0.15 y = (0.5 - 5z)/0.5 = (0.5 - 5(-0.15))/0.5 = 2.5 x = (5 - 2z + 9y)/4 = (5 - 2(-0.15) + 9(2.5) )/4 = 6.95
La solución es x = 6.95, y = 2.5 z = -0.15
Solución con rref(A) de Matlab
Con la matriz aumentada del sistema y con el comando rref(matriz) se resuelve el sistema
Introducir en MATLAB la información de la matriz aumentada:
>> A = [ 4 -9 2 5; 2 –4 6 3; 1 –1 3 4]
A =
4 -9 2 5
2 -4 6 3
1 -1 3 4
Utilizando el comando rref (A) se reduce la matriz aumentada a una matriz escalonada reducida cuya respuesta en forma de matriz diagonal es la solución del sistema propuesto.
>> rref(A)
ans =
1.0000 0 0 6.9500
0 1.0000 0 2.5000
0 0 1.0000 -0.1500
Programa Matlab para Gauss
La secuencia paso a paso se puede realizar en un archivo M como se muestra enseguida.
A = [4 -9 2 5;2 -4 6 3;1 -1 3 4 ] r1=A(1,:)/A(1,1) r2=A(2,:)-2*r1 r3=A(3,:)-r1 r2n=r2(1,:)/r2(1,2) r3n=r3-r3(1,2)*r2n z=r3n(1,4)/r3n(1,3) y=r2n(1,4)-r2n(1,3)*z x=r1(1,4)-r1(1,3)*z-r1(1,2)*y
El resultado es el mismo pero ahora en un programa que no utiliza el comando rref(A). Si existe alguna duda, consulta la lección sobre archivos M.