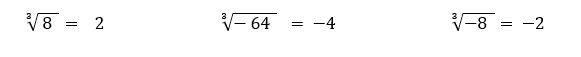El hombre aprendió a contar antes de aprender matemáticas, esto lo hizo a través de los números naturales. Asignó un número a cada objeto que poseía. Se dice que asigna un dedo a cada objeto, por ello el primer conjunto de números son llamados números naturales.
Números naturales
Inician con uno y van aumentando en incrementos de un entero.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 …
Contar con números cada vez más grandes no era problema, con el sistema arábigo sólo se requiere de diez dígitos y se van incrementando en decenas, centenas y millares.
Un problema se presenta cuando se van descontando números y se debe recurrir a los números enteros negativos.
Números enteros
Incluyen números negativos y positivos
-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7 …
Números racionales
Estos números surgieron de la necesidad de dividir un objeto en varios pedazos o fracciones, el ejemplo clásico habla de dividir un pastel en un determinado número de invitados. Por ello, los números racionales se definen como un grupo o conjunto de números que se expresan como la relación de dos números enteros, r = p/q.

Números irracionales
El teorema de Pitágoras resulto de un estudio griego, dijo Euclides «un triángulo rectángulo con catetos de una unidad de longitud e hipotenusa de longitud C, ver figura. Por el teorema de Pitágoras,

C2 = 12 + 12 = 2
Esto es, C = raiz(2), pero la cantidad raíz de 2, sea lo que sea, no es un número racional. Para decirlo en forma clara, si sólo existen números racionales, el triángulo rectángulo más sencillo que se conoce tiene una hipotenusa cuya longitud no se puede medir.
El argumento de Euclides utiliza a los números primos para solucionar esta interrogante.
Un número primo es un número natural que tiene exactamente dos números naturales como divisores, el mismo número y uno. Los primeros primos son
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Los números primos son los fundamentos para construir los demás números naturales. Por ejemplo,
18 = 2*3*3
40 = 2*2*2*5
Este tipo de factorización es posible para todos los números naturales no primos, mayores que uno.
Números reales
Los números son el conjunto de todos los números que pueden medir longitudes, junto con sus negativos y el cero. Así, los números racionales son automáticamente números reales; los números racionales positivos en efecto miden longitudes.
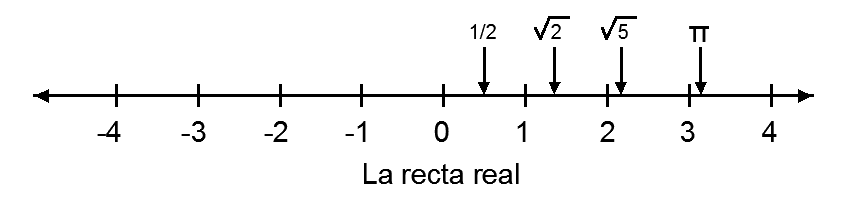
En una recta numérica calibrada y graduada, se podría pensar que todas las ranuras ya están etiquetadas, pero que ocurre con los puntos intermedios entre ranuras. Entre ranura y ranura pueden ubicarse también los números irracionales, como pi, raíz de 2, raíz de 5, etc.
Decimales
Hay otra manera importante de describir a los números reales, y es a través de los números decimales.
0.4 = 4/10 y 0.77=77/100
De manera similar

Si se continúa la división, se debe repetir un patrón. Así,
2/7 = 0.2857142857142857…
que también se puede escribir como
2/7 = 0.285714
Se puede colocar una barra sobre los números que se repite de forma indefinida.
¿Qué sucede con los decimales infinitos no periódicos, como 0.121121112111112 … ?
Representan a los números irracionales. Ellos, junto con los números racionales, constituyen a los números reales.
Un ejemplo de número irracional es raíz de 2 y que también tiene una expansión decimal.
raíz (2) = 1.414213…
Se conoce la expansión decimal de raíz de 2 hasta varios miles de cifras decimales y no tiene periodo alguno, no puede tenerlo. Es una verdad matemática.
Raíces cuadradas y cúbicas
Todo número positivo tiene dos raíces cuadradas. Por ejemplo, 3 y -3 son las raíces cuadradas de 9. Si a es un número positivo, raíz de a siempre denota la raíz cuadrada positiva de a. Entonces, raíz de 9 es 3, y las dos raíces cuadradas de 7 son raíz de 7 y menos raíz de 7.
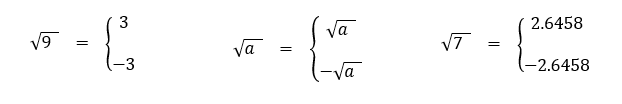
Por el momento, raíz de (-9) no tiene sentido pues no hay ningún número real cuyo cuadrado sea -9. Para que tenga sentido sacar la raíz cuadrada de un número negativo es necesario volver a extender el sistema numérico. Este tema se tratará en números complejos.
En contraste, la raíz cúbica de a , tiene sentido para cualquier número real a. Se cumple qué hay un único número real cuyo cubo es a. De esta manera raíz cúbica de 8 es 2, porque 2^3 = 8, y raíz cúbica de -64 es -4, ya que (-4)^3 = -64.