Las ecuaciones diferenciales ordinarias son algunas veces difíciles de resolver. MATLAB da una herramienta potente para ayudar a encontrar las soluciones de las ecuaciones diferenciales. La función dsolve calcula las soluciones simbólicas de ecuaciones diferenciales ordinarias.
La sintaxis es
donde eqn es la ecuación por resolver, ejemplo para resolver la ecuación diferencial
dy/dx = 3x
se emplea las siguientes instrucciones
syms y(x) a eqn = diff(y,x) == 3*(x) ySol(x) = dsolve(eqn)
El resultado es
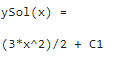
Se puede especificar la condición inicial, para y(0)=5
syms y(x) a eqn = diff(y,x) == 3*(x) cond= y(0)==1 ySol(x) = dsolve(eqn,cond)
La respuesta ahora es
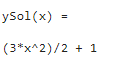
Las ecuaciones son especificadas con la letra D para indicar diferenciación.
La solución general de la ecuación de primer orden es la siguiente.

Resolviendo mediante la instrucción
dsolve (‘Dy = 1 + y^2’)
ans = tan(C1 + t)
donde C1 es una constante de integración.
Resolviendo la misma ecuación con la condición inicial y (0) = 10 se hallará
dsolve (‘Dy = 1 + y^2′,’y(0)=10’)
ans =
tan(t + atan(10))
De segundo orden
La diferencial de segundo orden se resuelve como
syms y(t) a eqn = diff(y,t,2) == a*y; ySol(t) = dsolve(eqn)
el resultado es
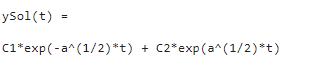
Resolviendo con las condiciones iniciales
syms y(t) eqn = diff(y,t,2) == 3^2*y; Dy = diff(y,t); cond = [y(0)==10, Dy(0)==1]; ySol(t) = dsolve(eqn,cond)
El resultado es
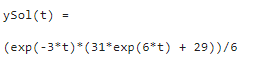
Para un sistema de tres ecuaciones diferenciales simultáneas se emplea
syms x(t) y(t) z(t)
eqns = [diff(x,t) == 15-0.3*x, diff(y,t) == 0.3*x-0.3*y, diff(z,t) == 0.3*y-0.3*z];
cond = [x(0)==30, y(0)==30,z(0)==30]
S = dsolve(eqns,cond)