En las lecciones anteriores se ha observado que MATLAB cuenta con varias instrucciones para gráficos y cálculos matemáticos simples. No obstante, también tiene otra colección de funciones predefinidas. Una de sus propiedades importantes es que operan directamente sobre cantidades escalares, vectoriales y matriciales. Por ejemplo, intenta con la matriz
A = [4 9; 25 81]
evaluar log(A)
El resultado es el cálculo del logaritmo natural para cada elemento como si se hubiera aplicado a un escalar.

Para indicar que la función logaritmo aplica a la matriz completa se debe indicar con una m al final del nombre de la función.
>> logm(A)
ans =
0.3119 0.4642
1.2894 4.2833
La mayoría de las funciones, como sqrt, abs, exp, operan de la misma forma para cada elemento o para un arreglo.
Para la función exponencial y la raíz cuadrada que ya conocimos, se aplica lo mismo.
La respuesta de Matlab para estos cálculos es
>> exp(A)
ans =
1.0e+035 *
0.0000 0.0000
0.0000 1.5061
>> sqrt(A)
ans =
2 3
5 9
>> expm(A)
ans =
1.0e+036 *
0.0861 0.2749
0.7636 2.4378
> sqrtm(A)
ans =
1.3620 0.8787
2.4409 8.8800
Aunque no todas las funciones que aplican para un elemento están definidas para una matriz
>> sin(A)
ans =
-0.7568 0.4121
-0.1324 – 0.6299
>> sinm(A)
??? Undefined command/function ‘sinm’.
abs(A)
ans =
4 9
25 81
>> absm(A)
??? Undefined command/function 'absm'
Otras funciones predefinidas para matrices son:
inv(A)
es una función que calcula la inversa de la matriz. También se obtiene la solución al emplear el operador de división matricial a la izquierda, x = A \ b.
det(A)
calcula el determinante de la matriz cuadrada A
eig(A)
calcula los valores propios asociados con la matriz cuadrada A.
lu (A)
calcula la factorización LU de la matriz A.
qr(A)
calcula la factorización QR de la matriz A.
svd(A)
calcula la descomposición en valores singulares de la matriz A.
rank(A)
devuelve el rango de la matriz A.
cond(A)
devuelve el número de condición de A.
norm(A)
calcula la norma de la matriz A.
poly(A)
encuentra el polinomio característico de la matriz A.
v=A(1,:)
n=min(v)
m=max(v)-min(v)
length(v)
Indica el número de elementos del vector v
diag(v)
crea una matriz cuadrada con los elementos de v en la diagonal
ones(n)
crea una matriz cuadrada con elementos iguales a uno
zeros(n)
crea una matriz cuadrada con elementos iguales a cero
eye(m,n)
crea una matriz identidad de tamaño mxn
mean(A)
determina el valor promedio de los elementos de la matriz o vector
sort(A)
ordena en forma ascendente los elementos de un vector
sum(A)
suma los elementos de un vector
trace(A)
suma los elementos de la diagonal de una matriz
Agregar columnas
A2=[6;2]
A=[A, A2]
Agregar renglones
A3=[10 21 5]
A=[A;A3]
Producto escalar y vectorial
a=A(1,:)
b=A(2,:)’
dot(a,b)
calcula el producto escalar de dos vectores del mismo tamaño
cross(a,b)
calcula el producto vectorial de dos vectores del mismo tamaño
Nuevas Funciones
Para declarar nuevas funciones se pueden utilizar el comando inline, una función anónima @(x), o una función externa llamada function a través de un archivo m. Veamos unos ejemplos,
Comando inline
Ejemplo:
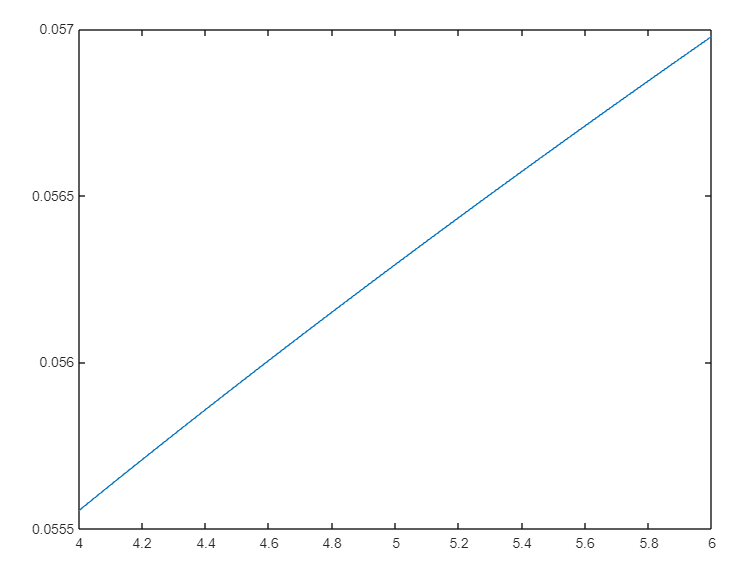
x= linspace(4,6);
f=inline ('1./(20-sqrt(x))');
y=f(x);
plot(x,y)
El resultado es una función cuya gráfica se observa enseguida:
También se puede utilizar función anónima (function handle @)
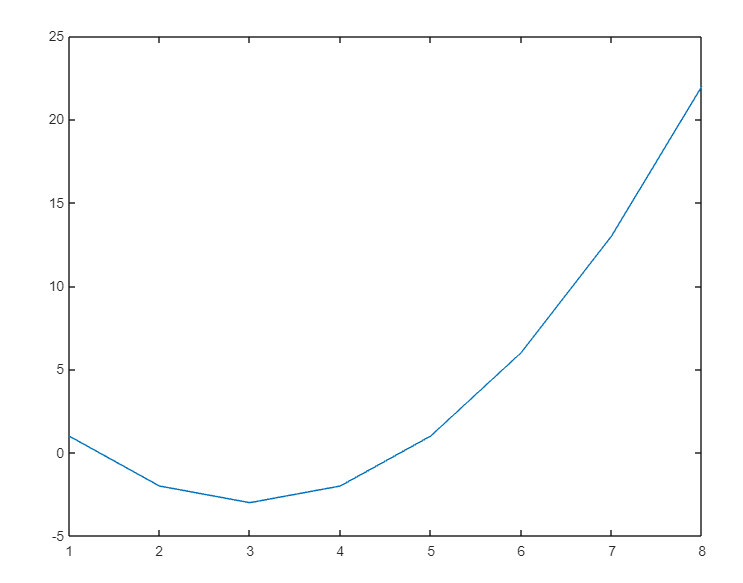
mifun = @(x) x.^2-3 dd=mifun(-2:5) plot(dd)
La función se grafica des -2 a 5 con el siguiente resultado
dd =
1 -2 -3 -2 1 6 13 22
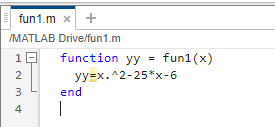
Otra forma es con el comando function que debe definirse en un script. Para utilizar la función se debe llamar a la función y colocar el argumento entre paréntesis.
Ejemplo
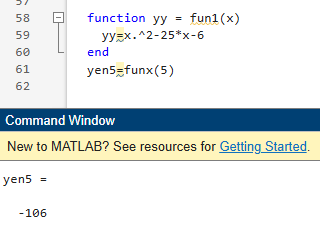
function yy = funx(x) yy=x.^2-25*x-6 end origen=funx(0)
Al guardar el archivo m se asigna el nombre de la función declarada. La función anterior se llama funx, y la siguiente se declara como fun1. Se pueden declarar tantas como se requieran.
Para hallar el valor sólo se utiliza el comando fun1(5) y el resultado es – 106
Se debe indicar el parámetro o valor de x para generar la respuesta.
Tarea 5
Elabore las siguientes funciones por cualquiera de las instrucciones descritas.
- Calcular la resistencia por la Ley de Ohm R=V/I. 120 volts y 12 amperes
- Cálculo de la presión por la ecuación de gas ideal PV = nRT. 20 mol, 600 K, 50 litros
- Determinar el Número de Reynolds, Re. Tubería de 1 pulgada, agua, 6 m/s, 22°C
- Calcular la Presión de oxígeno con Vander Waals, a 300 K, 37 litros, a = 8.78 bar.litros2/mol2, b = 0.0845 litro/mol. R = 0.08314 barL/molK