lecm8 Interpolación

La interpolación se define como la forma de estimar valores de una función entre aquellos dados por un conjunto de datos. La interpolación es una herramienta valiosa cuando no se puede evaluar rápidamente el valor de una función en puntos intermedios, existen múltiples métodos para hacer la interpolación dependiendo de la hipótesis que se haga. Más aún, es posible interpolar en más de una dimensión, como en el caso de la interpolación bidimensional.

Interpolación Lineal

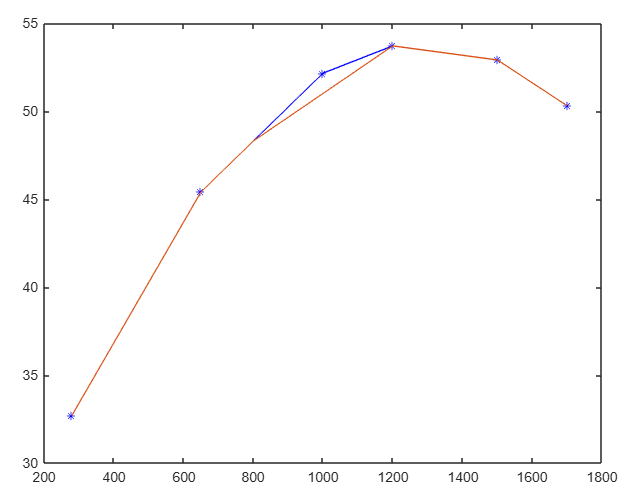
Tal como se muestra en las gráficas, MATLAB dibuja líneas que interpolan linealmente los puntos. Para estimar el Cp en cualquier momento dado se necesita usar la función interp1.
Los datos para este ejemplo se muestran en la siguiente tabla.

El calor específico del Permanganato de Potasio  a una temperatura de 800 K y utilizando la función interp1 en MATLAB proporciona 48.2929

t = [ 280, 650, 1000, 1200, 1500, 1700]
cp = [ 32.7, 45.4, 52.15, 53.7, 52.9, 50.3 ] ;

Cp800 = interp1( t, cp, 800) 


Cp800 =
 48.2929

Interpolación Bidimensional

La interpolación bidimensional se basa en las mismas ideas fundamentales que la interpolación unidimensional. Sin embargo, como su nombre lo indica, la interpolación bidimensional interpola funciones de dos variables, z = f (x, y). Para ilustrar esta dimensión, considérese el siguiente problema.
Las densidades de las soluciones acuosas del ácido sulfúrico varían con la temperatura y la concentración de acuerdo con la siguiente tabla:

Concentración (%)	10 °C	30 °C	60 °C	100 °C
5	1.0344	1.0281	1.0140	0.9888
20	1.1453	1.1335	1.1153	1.0885
40	1.3103	1.2953	1.2732	1.2446
70	1.6923	1.6014	1.5753	1.5417

El código de programación se debe elaborar con las siguientes instrucciones.

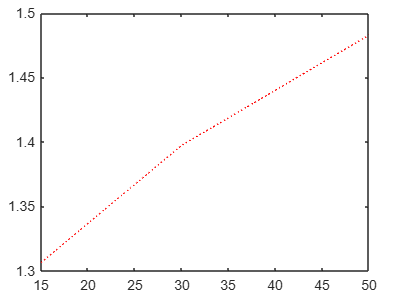
temp = [10 30 60 100];

conc = [5 20 40 70];

dens = [1.0344 1.0281 1.0140 0.9888; 1.1453 1.1335 1.1153 1.0885; 1.3103 1.2953 1.2732 1.2446; 1.6923 1.6014 1.5753 1.5417];

ti = [15 30 50]; 
ci=[40 50 60];

z= interp2(temp,conc,dens, ti, ci );

plot (ti,z,':')

El resultado es la siguiente gráfica

Otros métodos

Mínimos cuadrados

El método de mínimos cuadrados sirve para hallar un mejor ajuste de curvas  generadas a partir de un conjunto de datos. El término “mínimos cuadrados” es simplemente una forma abreviada de decir “minimizar la suma del error al cuadrado”. En MATLAB, la función polyfit resuelve el problema de ajuste  por mínimos cuadrados. Para ilustrar el uso de esta función, utilizar  el siguiente ejemplo.

La absorbancia de una sustancia varía con la concentración de glucosa de  acuerdo a la siguiente tabla.

Datos	1	2	3	4	5
mg glucosa	0	2	4	6	8
absorbancia	0.002	0.150	0.294	0.434	0.570

Para usar polyfit se deben dar los datos y el orden que mejor se ajuste a los datos. Si elige n = 1 como el orden, se encontrara la mejor aproximación líneal. Esto se llama “regresión lineal”. Por otra parte si designa n = 2, se buscará  un “polinomio cuadrático”.

Para los datos tabulados, se observa que se debe utilizar un polinomio con curvatura en vez de una recta.

Introduciendo está información como polinomios en MATLAB se procede a obtener el polinomio de interpolación por el método de mínimos cuadrados.

Se carga la información necesaria en MATLAB como son los datos de la glucosa y absorbancia.

glu = [0  2  4  6  8];

>> ab = [0.002  0.15  0.294  0.434  0.57];

En este caso, glucosa es la variable independiente (abscisa) y el contenido de absorbancia es la variable dependiente (ordenada).

En MATLAB se carga el orden del polinomio de ajuste o regresión:

>> n = 2;

La función polyfit de MATLAB ajusta  el  polinomio de segundo grado a los datos de concentración de glucosa  y absorbancia

>> p = polyfit(glu, ab, n);

p =

-0.0005    0.0750    0.0020

La salida de polyfit es un vector  fila de los coeficientes de los polinomios. En este caso la solución es:

y =  -0.0005x² + 0.075x  +  0.002

Para  comparar la solución del ajuste de curvas a los datos, represente gráficamente  ambos:

>> ti = linspace ( 0, 8, 2 );

Crea el eje  x  para representar el polinomio.

z = polyval ( p, ti );

Llama a la función  polyval  de MATLAB para evaluar el polinomio p con los datos en ti.

>> plot(glu,ab,glu,ab,’o’,ti,z,’:’);

La figura que se obtiene representa los datos originales  x  e y  marcando los datos con ‘o ‘;  después, se representan otra vez  los datos originales dibujando líneas rectas entre ellos y los polinomios ti y  z  usando una línea a tramos. Se completa la  gráfica con las etiquetas y el título de la figura.

>>xlabel ( ‘ concentración ‘ )

>>ylabel (‘ absorbancia ‘ )

>>title (‘Variación de la absorbancia con la concentración de glucosa’ )

La gráfica que se obtiene con ajuste cuadrático, n = 2 se muestra en siguiente figura. Siendo el polinomio de ajuste cuadrático

p =   – 0.0005x² + 0.075x  +  0.002