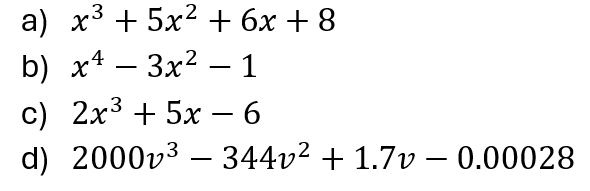Hay muchas funciones de MATLAB que permiten operar sobre los arreglos como si sus entradas fueran coeficientes o raíces de ecuaciones polinomiales. Por ejemplo, introduce
>> c = [ 1 -15 59 -81 36 ]
después
>> r = roots( c)
Con ello, las raíces del polinomio x4 –15x3 + 59x2 – 81x + 36 se imprimirán y además se almacenaran en el vector r. De acuerdo al polinomio anterior las raíces del polinomio c son:

Una vez encontradas las raíces del polinomio MATLAB dice que estas raíces son vectores columna.
Siguiente ejemplo. Sea el polinomio x4 –16x3 + 22x + 116, hallar sus raíces.
En este caso se deben introducir en MATLAB también los términos nulos ya que MATLAB no tiene forma de saber cuáles son a menos que se indiquen, por lo tanto el polinomio se introduce como:
p = [1 –16 0 22 116] r = roots (p)
resultado

Dos de las raíces son complejas, y MATLAB trabaja indistintamente con números reales y complejos. Prueba multiplicar r(3)*r(4) y el resultado debe ser un número real (3.1759).
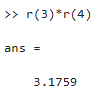
Búsqueda de raíces
fzero
Es otra función que se utiliza para hallar la raíz de una función no lineal. Uitliza el método de bisección. Se requiere de la función y de un valor inicial de aproximación.
x = fzero(fun,x0)f1=inline('x.^4-15*x.^3+59*x.^2-81*x+36')
z = fzero(f1,2)
La respuesta es z = 1.2280

Con distintos valores iniciales se exploran o buscan las distintas raíces reales de la función.
z = fzero(f1,5)
z = 3.0000
z = fzero(f1,0)
z = 3.0000
z = fzero(f1,10)
z = 9.7720
Gráfica de función con fplot
Con esta función se puede explorar el trazo de los datos, se declara la función anónima con @ y también se puede establecer los límites inferior y superior.
fplot(@(x) x.^4-15*x.^3+59*x.^2-81*x+36)
produce la figura
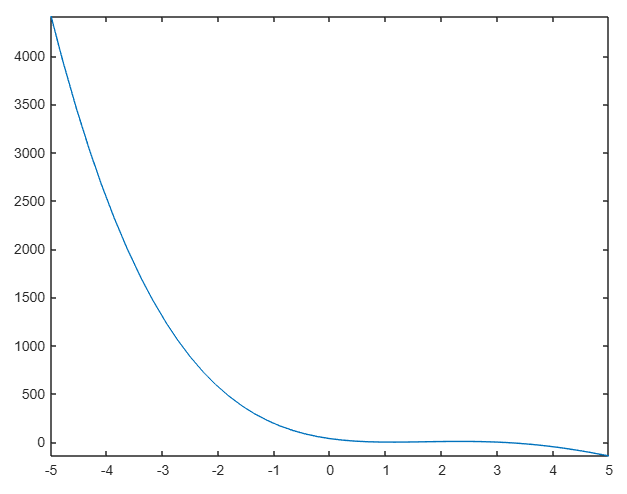
Para un intervalo de [0,10] se utiliza la instrucción
fplot(@(x) x.^4-15*x.^3+59*x.^2-81*x+36,[0,10])
el resultado es
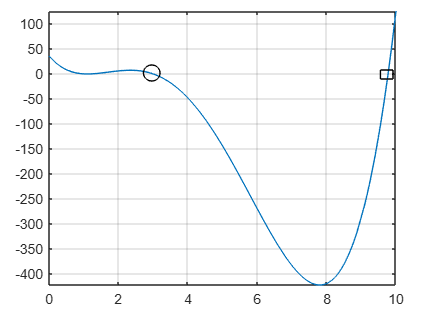
En el circulo se encuentra la primer raíz y en el rectángulo la segunda raíz.
Función Solve
Solve resuelve una ecuación o un sistema de ecuaciones, se debe dar también una ecuación y el valor inicial de búsqueda.
Utilicemos Solve para encontrar las raíces del polinomio
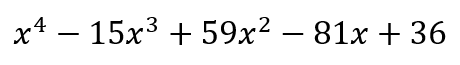
Sus raíces son
p1=[1 -15 59 -81 36] r1=roots(p1)

Para utilizar la función solve se debe definir una variable simbólica, para este ejemplo se utilizará la letra t y como valor inicial cero.

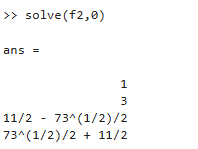
Para mejorar la presentación de la respuesta utilizamos la instrucción double(x)

Utilizando la función fplot observamos las primeras raíces .
fplot(@(x) x.^4-15*x.^3+59*x.^2-81*x+36,[0,3.5])
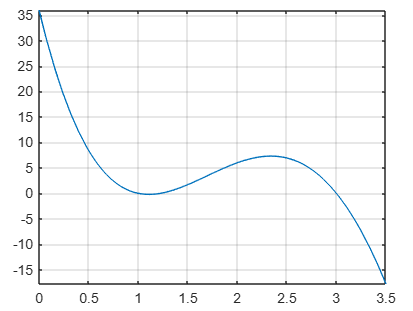
La otra raíz se observa mejor con
fplot(@(x) x.^4-15*x.^3+59*x.^2-81*x+36,[4,10])
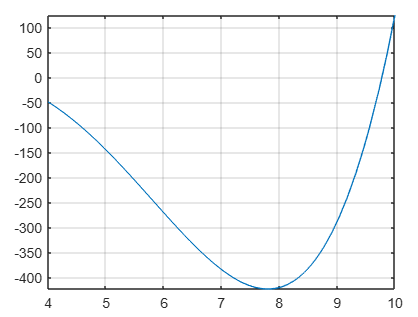
Tarea 7
Determine las raíces de las siguientes funciones