En Matlab hay funciones definidas para determinar la raíz de un dato, calcular el seno, coseno y tangente de un número. Se obtiene el determinante, la inversa y el rango de una matriz a través de las funciones det(x), inv(x) y rank(x). Todas las funciones que se mencionan son funciones internas de Matlab.
El usuario puede definir la función que desee con ayuda de un archivo M.
Las funciones definidas por el usuario se almacenan como archivos-m y Matlab puede acceder a ellas si están almacenadas en el directorio actual.
La sintaxis de la declaración es

Ejemplo, con la función function que debe definirse en un script y llamar al archivo funx.m
function yy = funx(x)
yy=x.^2-25*x-6
end
Para hallar el valor sólo se utiliza el comando xx=funx(3) y el resultado es -72
Otro ejemplo, para calcular el área de un cilindro se debe declarar la función
function area_cil = acil(r,h)
% calcula el área de un cilindro
% ingresar radio y altura en cm
% se calcula el área en cm^2
a1=pi()*r*h
fprintf ('El área del cilindro es %6.2f \n', a1)
Al guardar el archivo se almacena la función acil y se deben ingresar dos parámetros
acil(2,5)
El resultado es

Funciones inline
Para declarar nuevas funciones se pueden utilizar:
Comando inline
Ejemplo:
x= linspace(4,6;
f=inline ('1./(20-sqrt(x))');
y=f(x);
plot(x,y)
También se puede utilizar función anónima (function handle @)
mifun = @(x) x.^2-3 dd=mifun(2:4)
Uso de las funciones externas
Al evaluar un sistema de ecuaciones diferenciales el empleo de los archivos M y la declaración de función del usuario ofrecen mayor potencialidad a Matlab. Este tipo de archivo es independiente e inicia con el comando function. A continuación se da un ejemplo aplicándolo a un sistema de ecuaciones diferenciales ordinarias y resolviendo el sistema por medio del método de Runge Kutta de cuarto orden.
Enunciado del problema
Se tienen tres tanques de 1000 litros de capacidad. Los tres recipientes están completamente llenos y perfectamente agitados con una solución cuya concentración es 30 g/l. A partir de cierto momento se alimenta al primer tanque una solución que contiene 50 g/l con un gasto de 300 l/min (hay un arreglo entre los tres recipientes tal que al haber un gasto al primero, la misma cantidad fluye de este al segundo, del segundo al tercero y de este afuera del sistema, con lo cual se mantiene constante el volumen en todos ellos). Determinar las concentraciones en cada tanque
después de los 10 minutos de haber empezado agregar solución al primero.
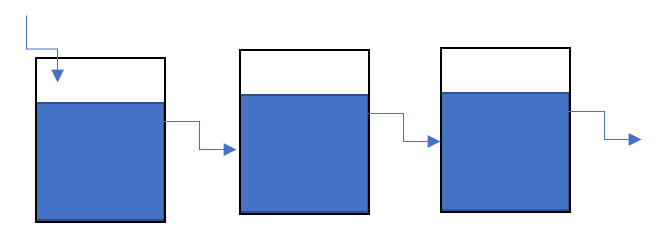
Solución:
Balance de soluto en el primer tanque
Acumulación = Entrada – Salida
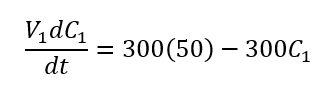
como V1 = 1000 y permanecen constantes
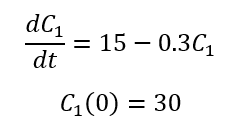
Balance de soluto en el segundo tanque
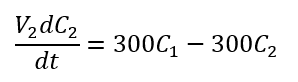
Como V2 = 1000 litros
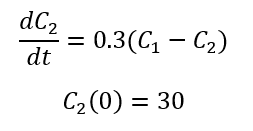
Balance de soluto en el tercer tanque
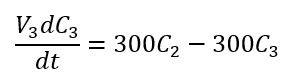
Como V3 = 1000 litros
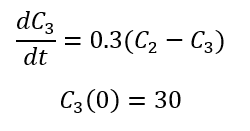
El sistema de ecuaciones diferenciales resultante es:

Una vez que se tienen las ecuaciones para cada uno de los tanques se escriben un archivo-M de la siguiente forma:
function otra = mezcla (t,x) otra =[15-0.3*x(1);0.3*x(1)-0.3*x(2);0.3*x(2)-0.3*x(3)];
En la ventana de comando de Matlab escriba las siguientes líneas y observará la gráfica del sistema.
>>t=0:10;
>>x=[30,30,30];
>> [t,y]=ode45('mezcla',t,x)
>> plot(t,y,'o',t,y,'-')
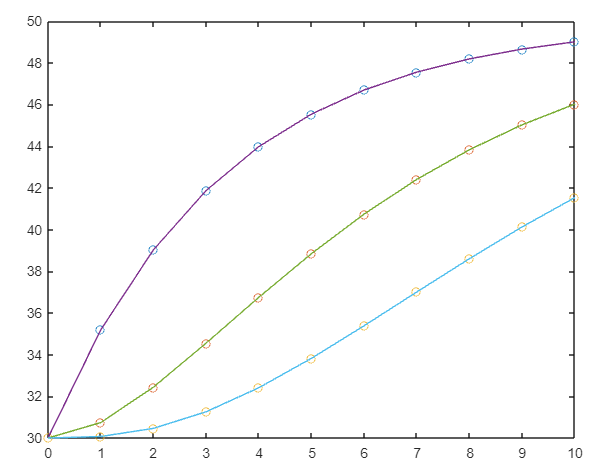
Matlab da el resultado de las concentraciones de cada tanque de 0 a 10 minutos después de haber agregado la solución al primero.
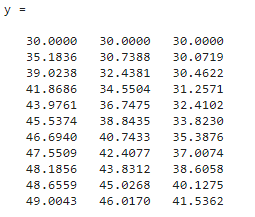
La gráfica resultante se muestra enseguida.