La función de integración int( f ), donde f es una expresión simbólica, intenta obtener otra expresión simbólica f tal que diff( f) = f, la integral es más complicada que la diferenciación. La integral o antiderivada puede no existir en forma cerrada o puede existir pero el software no puede encontrarla. cuando MATLAB no logra encontrar la anitderivada, devuelve el comando sin evaluarlo.
La función int se usa para expresar la función simbólica, se puede usar argumentos opcionales para especificar la variable simbólica y los límites de una integral definida.
Integración Simbólica
Crea la función simbólica

syms s x z
z = cos(s + 2*x)
- Integra con respecto a la variable independiente x

int(z)

- Integra con respecto a s

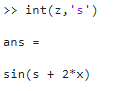
- Crea una función simbólica

- Integra con respecto a la variable x


Integración Numérica
Con MATLAB es posible resolver integrales definidas de tipo numérico.

Hay varios métodos de integración numérica, y son llamados cuadratura numérica en donde MATLAB requiere de la función quad, con dicha función podemos obtener los valores de la integral g, y con la función trapz MATLAB calcula la integral usando la regla del trapezoide, estas funciones pueden ser útiles cuando hay sólo puntos discretos de datos en la integral.
Integrales con Trapecios
trapz (x, y)
Calcula la integral de y como una función de x. Los vectores de x y y tienen la misma longitud (xi, yi) representan los puntos sobre la curva. Por ejemplo:
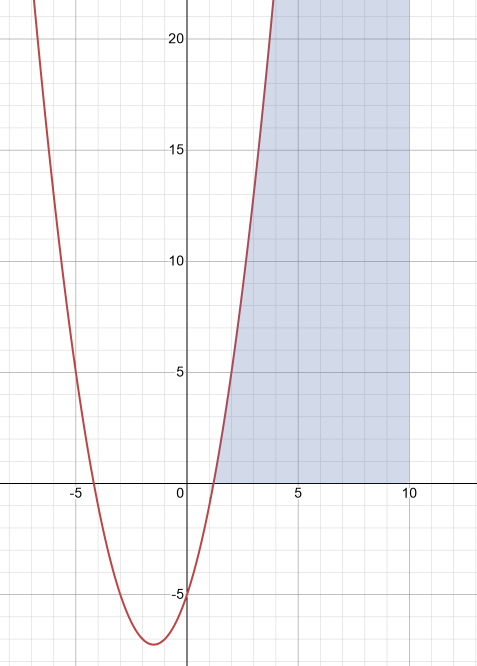
x = 1:10
g = x.^2 + 3*x – 5
trapz(g)

La gráfica es
El espacio entre los puntos no tiene que ser equidistante y el valor de x no tiene que ser almacenado, sin embargo, los intervalos negativos son considerados como una integral negativa. Por ejemplo,
y=-5:5
y =
-5 -4 -3 -2 -1 0 1 2 3 4 5
g=y.^2+3*y-5
g =
5 -1 -5 -7 -7 -5 -1 5 13 23 35
trapz(g)
ans =
35
La integral resultante es I = 100/3

La primera y tercera parte son positivas, y la segunda parte es negativa
I = I1 – I2 + I3
I total = 1.9308 – 26.028 + 57.4308 = 33.333
Ejercicio
Calcule la integral siguiente con diferentes métodos de MATLAB

Resolviendo por el método del trapezoide.
Primero hay que crear un vector con valores de x entre 0 y 1
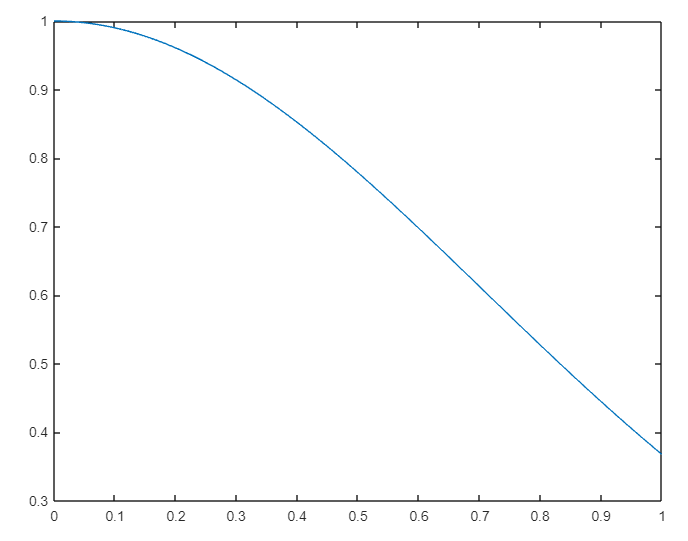
x=linspace(0,1);
luego se emplea obtiene un vector y como una función de x
y=exp(-x.^2);
Una vez establecidos los datos a MATLAB la integral puede calcularse
integral=trapz(x,y)
integral =
0.7468
la gráfica correspondiente es
Ejercicios. Calcule la siguiente integral

La representación y solución en MATLAB es

Calcule la siguiente integral con MATLAB

La representación y solución en MATLAB es
