Métodos de Solución

Temario de Métodos Numéricos

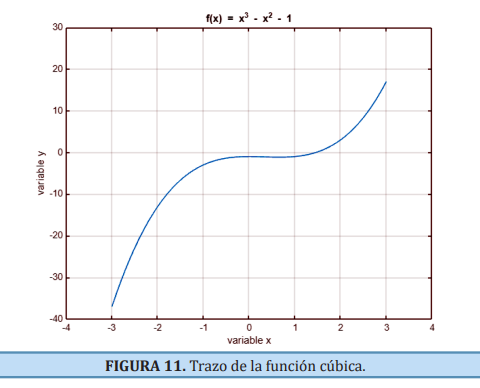
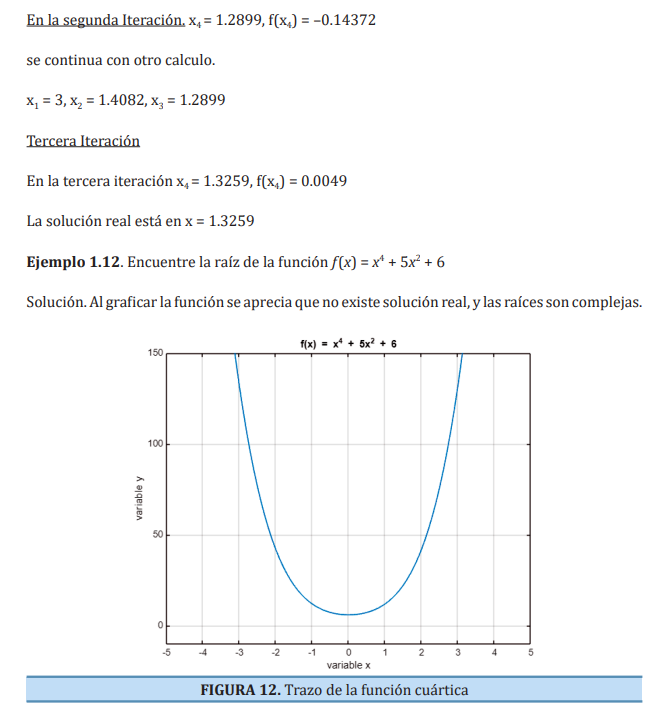
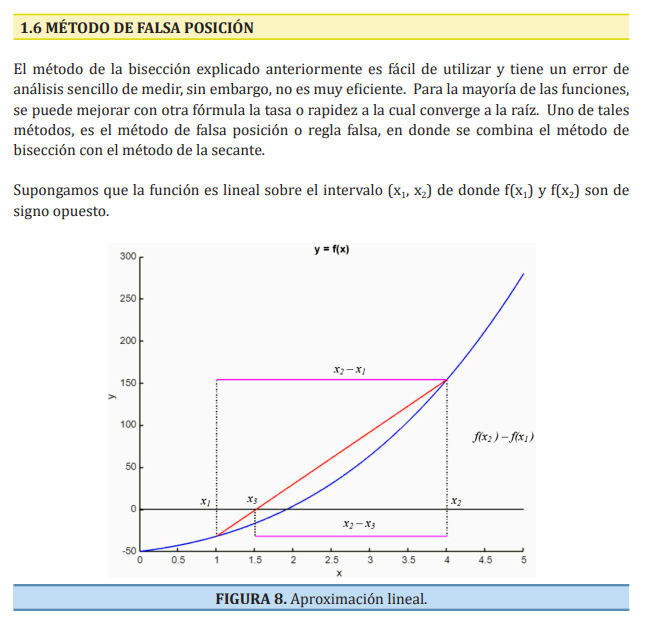
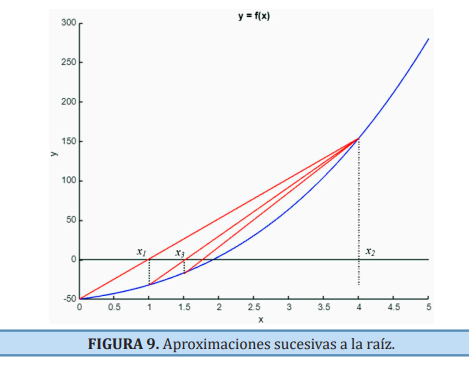
La asignatura de Métodos Numéricos tiene como objetivos.

Objetivo general:
El alumno será capaz de seleccionar, implementar y aplicar los métodos numéricos en los diferentes problemas específicos que se desarrollen.

Objetivo específico:
Analizar los métodos numéricos que constituyen algoritmos mediante los cuales sea posible formular problemas matemáticos, para que se puedan resolver, utilizando operaciones aritméticas.

Contenido

Unidades	Tema y subtemas
1. Introducción	1.1 Papel de los métodos numéricos en la ciencia y la ingeniería. 1.2 Breve panorama histórico 1.3 Lenguajes de programación 1.4 Problemas típicos
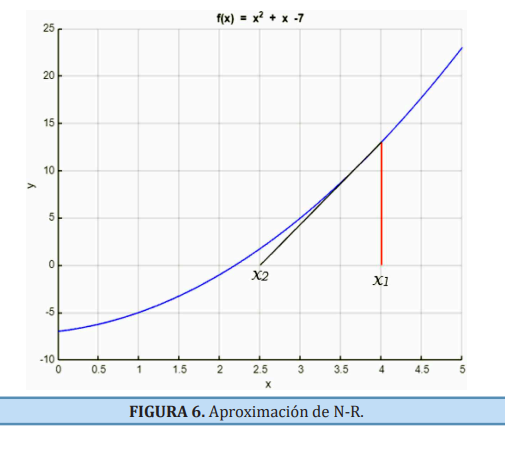
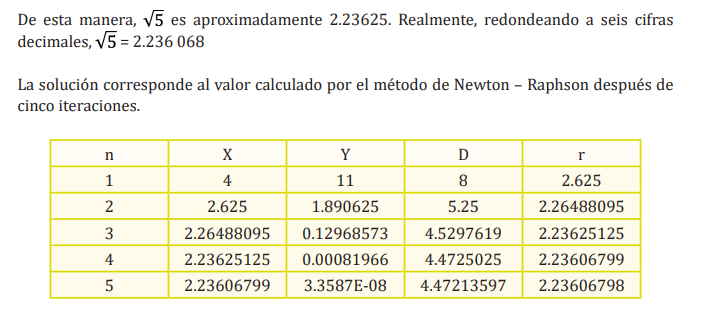
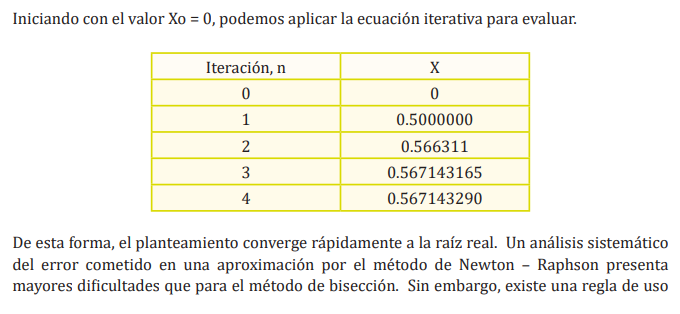
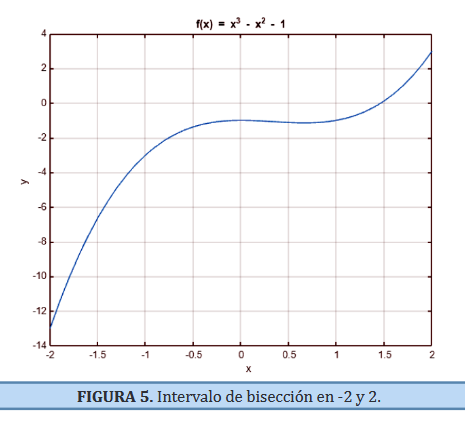
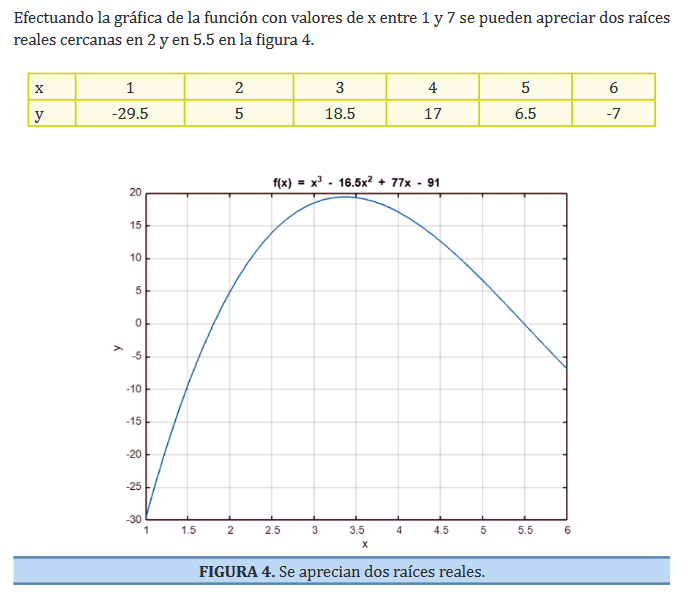
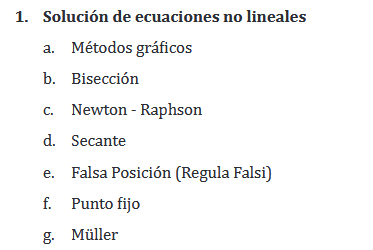
2 Evaluación de Funciones	2.1 Raíces de una ecuación (Gráfico) 2.2 Bisección 2.3 Newton – Raphson 2.4 Secante 2.5 Regla falsa 2.6 Punto fijo 2.7 Muller
3 Sistemas de ecuaciones lineales y no lineales	3.1 Método de Cramer 3.2 Método de Gauss 3.3 Método de Gauss – Jordan 3.4 Método de Gauss – Zamora 3.5 Método de Gauss – Seidel 3.6 Inversa de una matriz. 3.7 Newton Multivariable 3.8 Método de Broyden
4 Interpolación	4.1 Interpolación 4.2 Mínimos cuadrados 4.3 Polinomio simple 4.4 Polinomio de Lagrange 4.5 Diferencias finitas (Newton)
5 Integración y derivación	5.1 Integración numérica 5.2 Regla del trapecio 5.3 Reglas de simpson 5.4 Cuadratura de Gauss 5.5 Derivación numérica
6 Ecuaciones diferenciales ordinarias	6.1 Serie de Taylor 6.2 Euler simple y modificado 6.3 Runge – Kutta