- Teorema del Factor
- Teorema del Residuo
- Teorema fundamental del álgebra
- Teorema de Abel
- Regla de Descartes
Teorema del factor
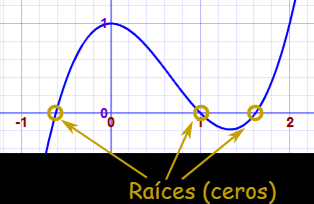
En álgebra, el teorema del factor sirve para encontrar los factores de un polinomio. Es un caso especial del teorema del resto. Este polinomio y=-x4+3x3-4x, con raíces en: x=-1, x=0 y x=2 Se factoriza como -(x+1)(x)(x-2)2.
Si a = -1, f(a) = f(-1) = – (-1)4 + 3(-1)3 – 4(-1) = – 1 – 3 + 4 = 0
Dividiendo a y=-x4+3x3-4x, con (x – a) se obtiene como residuo 0.

Teorema del residuo
Y el teorema del residuo establece que si un polinomio de x, f(x) , se divide entre (x – a) , donde a es cualquier número real o complejo, entonces el residuo es f(a) . Esto significa que para encontrar el residuo cuando un polinomio es dividido entre un binomio el valor de x es igual al valor a, o f(x) = f(a) .
con a = 3, f(x) = f(3) = – (3)4 + 3(3)3 – 4(3) = – 81 + 81 – 12 = – 12

Teorema fundamental del álgebra
El teorema fundamental del álgebra establece que “Una función polinomial de grado n th tiene exactamente n ceros en el conjunto de números complejos, contando ceros repetidos .” Iguale g ( x ) = 0 y factorice los números complejos para encontrar los ceros.
Teorema de Abel
El teorema de Abel, afirma que no existe una combinación finita de radicales y funciones racionales que solucionen la ecuación algebraica genérica de grado 5 (o mayor que 5), es uno de los primeros y más importantes resultados de imposibilidad en matemáticas.”
Regla de Descartes
La regla de los signos de Descartes nos ayuda a identificar el número posible de raíces reales de un polinomio p (x) sin graficar o resolverlas realmente. Esta regla no proporciona el número exacto de raíces del polinomio ni identifica las raíces del polinomio. Por ejemplo,
Tiene un cambio de signo entre el segundo y el tercer término. Por tanto existe solamente una raíz positiva según Descartes.
Las raíces son 1, -1 y -1.

