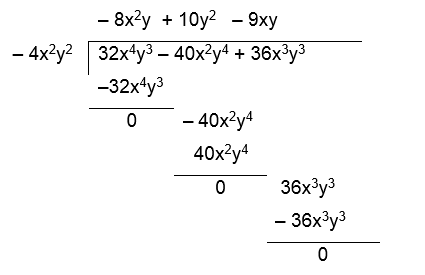mn0e Polinomios

Teorema fundamental del álgebra

• Toda ecuación polinomial de grado n >= 1 tiene al menos una raíz, real o imaginaria.
• Toda ecuación polinomial f(x) = 0 de grado n tiene exactamente n raíces. Las raíces pueden ser reales, reales repetidas y complejas.
• Todo polinomio f(x) de grado n >= 1 se puede expresar como el producto de n factores lineales.
• Si un número complejo a + bi es una raíz de la ecuación polinomial con coeficientes reales y con b distinto de cero, entonces su complejo conjugado a – bi también es una raíz.

Esto se muestra con los siguientes polinomios:

Operaciones con polinomios

Producto de polinomios

Para multiplicar dos polinomios, se multiplica cada uno de los términos de un polinomio por los términos del otro polinomio y se suman los productos parciales.

Para facilitar la operación, conviene en la mayoría de los casos, hacer el producto observando lo siguiente.

1. Ordenar el multiplicando y el multiplicador en el mismo sentido de una letra de mayor a menor grado.
2. Escribir el producto parcial debajo de cada término.
3. Escribir en una misma línea e identificar términos semejantes.
4. Efectuar la reducción de términos semejantes.

Ejemplo. Multiplicar los polinomios

a³ + 4a + 2a² + 6 con a² + 3 + 7a

Ordenando por términos en relación a la variable a.

a³ + 2a² + 4a + 6 con a² + 7a + 3

Resolver productos término a término

Realizar las siguientes multiplicaciones:

---

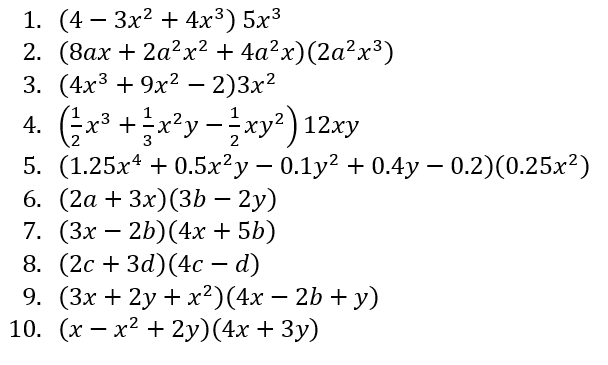
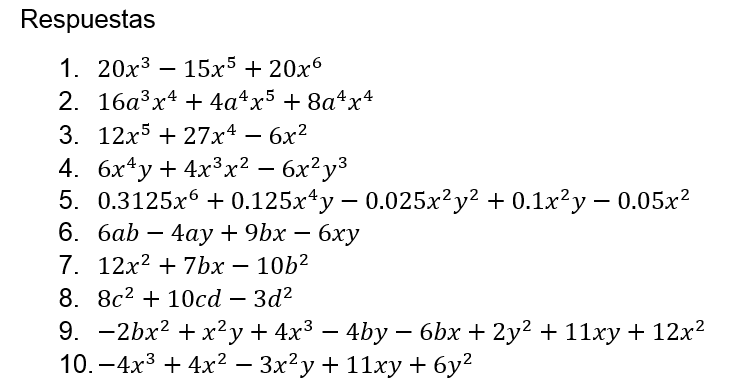
División de un polinomio por un monomio

Para esta división se divide cada uno de los términos del polinomio entre el monomio.

Ejemplo. Dividir 32x⁴y³ – 40x²y⁴ + 36x³y³ por – 4x²y²

32x⁴y³/ – 4x²y² = – 8x²y

– 40x²y⁴/ – 4x²y² = 10y²

36x³y³/ – 4x²y² = – 9xy

El resultado es: -8x²y + 10y²– 9xy