Simpson 1/3

Además de la regla del trapecio, otra manera de obtener una estimación más exacta de una integral es utilizar polinomios de orden superior para conectar los puntos. Por ejemplo, se pueden conectar con un polinomio de tercer orden los puntos f(a), f(b) y el punto medio entre ellos.

A las fórmulas que resultan de calcular la integral bajo estos polinomios se les llama reglas de Simpson.
Con la regla de Simpson es posible obtener una aproximación más precisa del área bajo una curva ya que se conectan grupos sucesivos de tres puntos sobre la curva mediante parábolas de segundo grado, y al sumar las áreas bajo las parábolas se obtiene el área aproximada bajo la curva.

Esta regla a diferencia de la regla del trapecio, donde a mayor número de subdivisiones se obtiene una mejor aproximación, lo que hace es ajustar una curva de orden superior en lugar de la línea recta como sucede con la regla del trapecio.

Suponga que se tiene la función f(x) = x^3 – 6x + 3 y los siguientes datos:

a	f(a)	m = (a+b)/2	f(m)	b	f(b)
2	-1	3.5	24.875	5	98

La regla de Simpson utiliza la fórmula

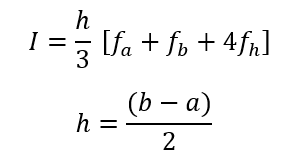
Entonces, sustituyendo valores

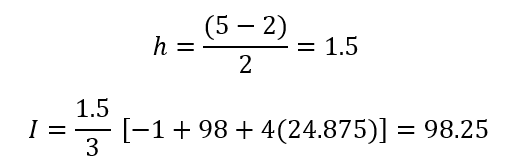
Ejemplo