Variables en forma de vector y matriz
Parte importante del uso de Matlab es la manipulación y almacenamiento de datos en tablas. Las tablas de una columna o una fila se almacenan en vectores, y las tablas con varias columnas y renglones se almacenan en matrices. La tabla siguiente de tiempo contra temperaturas se puede almacenar en dos vectores o en una matriz.
| Tiempo (min) | 0 | 4 | 8 | 12 | 16 |
|---|---|---|---|---|---|
| Temperatura (°C) | 25 | 32 | 38 | 45 | 64 |
Un vector es una colección de elementos.
El vector renglón se asigna como t = [0 4 8 12 16].
Se puede almacenar en dos variables como
t = [0 4 8 12 16]
T = [25 32 38 45 64]
O en una sola en forma matricial
tabla = [0, 4, 8, 12, 16; 25, 32, 38, 45, 64]
El resultado en la ventana de comandos es

Los elementos del vector deben ir separados por espacios o por comas, t = [0, 4, 8, 12, 16].
En ambos formatos la variable t almacena cinco elementos en arreglo horizontal. Para el otro vector el arreglo es similar.
T = [25, 32, 38, 45, 64]
La matriz denominada tabla es un arreglo rectangular de 2 renglones por 5 columnas, (2×5). Es importante observar que los elementos de un vector o una matriz van encerrados entre corchetes. Un espacio o una coma separa a cada uno de los elementos; y el punto y coma separa los elementos entre un renglón y otro.
Para declarar una colección de elementos en arreglo vertical se debe declarar un vector columna. Aquí se requiere que los elementos vayan encerrados entre corchetes y separados por punto y coma.
T = [25; 32; 38; 45; 64]
También se puede transponer un vector renglón con el operador apostrofo al final.

Para obtener una lista de todas las variables usadas hasta el momento se emplea el comando who o si se quiere con más detalle se emplea whos.

Luego de haber realizado varios cálculos, es momento de limpiar la pantalla. Para ello debes utilizar el comando clc.
Observa que si ahora se utiliza whos, las variables siguen guardando la información y sólo se limpia la pantalla.

Borrar Variables
Si ahora utilizas el comando clear y verificas la información almacenada con el comando whos, notaras que todas las variables han sido eliminadas de la memoria.

Advertencia. Recuerda que los comandos limpiar pantalla (clc) y limpiar memoria (clear) deben ser utilizados con cuidado para evitar perder información o efectuar cálculos erróneos. También, recuerda que el verdadero potencial de MATLAB se demuestra en la capacidad para realizar cálculos utilizando vectores y matrices.
Operaciones entre matrices
Es fácil realizar suma, multiplicación y división entre matrices.
SUMA. La suma de dos matrices de la misma dimensión es aquella matriz cuyos elementos son la suma de los elementos correspondientes.
>>K=[22 14; 46 13] >>L=[41 27;62 18] >>K + L
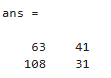
La principal restricción para poder sumar dos matrices es que las matrices deben ser del mismo tamaño (A m×n). No se puede sumar una matriz de 4 x 3 con una de 6 x 2, aun cuando ambas tengan 12 entradas.
RESTA. La operación es similar a la suma.
>>K - L
ans =
-19 -13
-16 -5
MULTIPLICACIÓN. El producto de una matriz Am×n y una matriz Bn×p es la matriz Cm×p, cuyo elemento en el renglón m y columna p, es la suma de los productos de los elementos correspondientes. A manera de ejemplo.
Sea A = [1 2 1; 4 1 5] y B = [1 2 3; 3 1 -1; 1 4 2] calcular el producto AB
La operación elemento por elemento es
| (1)(1) + (2)*(3) + (1)*(1) | (1)(2) + (2)*(1) + (1)*(4) | (1)(3) + (2)*(-1) + (1)*(2) |
| (4)(1) + (1)*(3) + (5)*(1) | (4)(2) + (1)*(1) + (5)*(4) | (4)(3) + (1)*(-1) + (5)*(2) |
El resultado es
| 8 | 8 | 3 |
| 12 | 29 | 21 |
El código y el resultado que se obtiene es
clc A=[1 2 1;4 1 5] B=[1 2 3;3 1 -1;1 4 2] A*B

Para ilustrar otra multiplicación de vectores, ahora defina a los vectores a y b como, a = [ 1 3 3] y b = [4 5 6]’. También defina la matriz A = [1 2 3; 4 3 1; 7 8 9]
a = [ 1 3 3] b = [4 5 6]' A = [1 2 3; 4 3 1; 7 8 9]
Una vez definidas, realice las operaciones a*b y b*a
a*b
ans =
37
b*a
ans =
4 12 12
5 15 15
6 18 18
El primer producto es el producto punto de vectores cuyo resultado es un escalar.
a*b = (1)(4) + (3)(5) + (3)(6) = 37
El segundo producto b*a es el producto cruz cuyo resultado es una matriz.
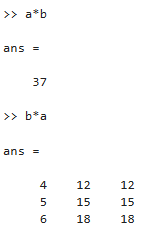
Después, intenta con a*A o A*b
a*A
ans =
34 35 33
A*b
ans =
32
37
122
Estos productos vector-matriz y matriz-vector generan un vector.
¿Qué ocurre cuando las dimensiones no son las requeridas por las operaciones?
Para verlo, escriba A*a
>> A*a Error using * Incorrect dimensions for matrix multiplication. Check that the number of columns in the first matrix matches the number of rows in the second matrix. To perform elementwise multiplication, use '.*'.
La operación no se realiza debido a que las dimensiones de las matrices son distintas.
Utilizando el operador .* se realiza la operación elemento a elemento y se obtiene el producto.
>> A.*a
ans =
1 6 9
4 9 3
7 24 27
La multiplicación matriz-matriz se lleva a cabo de la misma forma que A*A
>> A*A
ans =
30 32 32
23 25 24
102 110 110
También son posibles las operaciones con escalares: A / pi
>> A/pi
ans =
0.3183 0.6366 0.9549
1.2732 0.9549 0.3183
2.2282 2.5465 2.8648
Es importante recordar siempre que MATLAB aplicara las operaciones aritméticas simples en forma de vectores y matrices, si es posible. En ocasiones, se querrá llevar a cabo el cálculo paso por paso en una matriz o vector. MATLAB también puede hacer eso. Por ejemplo, A^2 da como resultado una multiplicación matricial de A = [1 2 3; 4 3 1; 7 8 9] consigo misma. El resultado es A*A
>> A^2
ans =
30 32 32
23 25 24
102 110 110
Pero, ¿Qué hacer si quiere elevar al cuadrado cada elemento de A? Esto se puede hacer con el operador punto de la siguiente manera A .^ 2
>>A.^2
ans =
1 4 9
16 9 1
49 64 81
El punto que precede al operador ^ significa que la operación será llevada a cabo elemento a elemento. El manual de MATLAB llama a éstas operaciones entre arreglos.
Edición de elementos de una matriz
Para la exposición de este tema inicie con la designación de un vector renglón
>> A = [4 5 6]
A =
4 5 6
Para agregar otra fila se teclea el primer vector seguido de un punto y coma, posteriormente se teclea el segundo vector dejando espacio entre número y número. De esta forma se puede escribir el número de filas deseadas como sigue:
A = [A; 1 3 2]
A =
4 5 6
1 3 2
El punto y coma dentro después del vector inicial indica que los siguientes elementos se agregan a la linea siguiente. Cada ; separa las filas y los espacios separan a los elementos.
A=[A;1 3 2 0] Error using vertcat Dimensions of arrays being concatenated are not consistent.
Produce error porque se intenta adicionar 4 elementos a un vector inicial de 3.
Se pueden agregar varias lineas o columnas. Por ejemplo,
A(1,4)= 0
A =
4 5 6 0
1 3 2 0
A(4,3)= 1
A =
4 5 6 0
1 3 2 0
0 0 0 0
0 0 1 0
Adiciona una columna y coloca ceros en las entradas, en la posición (4,3) asigna el valor de 1 y rellena los otros lugares con ceros.
Otra forma de construir un vector renglón en MATLAB es de la siguiente forma
>> A = [ 2 : 6 ]
A =
2 3 4 5 6
En este caso los dos puntos ( : ) son un operador general, con ellos se puede entender como desde… hasta. En el ejemplo anterior la orden para MATLAB fue crear un vector fila desde 2 hasta 6.
La construcción de un vector columna en MATLAB es de la siguiente forma:
>> B = [ 2: 6 ]’
y MATLAB responde
B =
2
3
4
5
6
Otra forma de construir un vector columna es:
>>A = [7; 5; 3]
A =
7
5
3
Si quisiera cambiar un elemento de alguna columna o fila se escribe la posición del elemento en la fila y columna correspondiente. Por ejemplo, en la matriz
C = [1 5 4;3 2 6;9 8 1]
el número 8 se ubica en la posición C(3, 2). Para comprobarlo se escribe C(3,2) y se mostrará el número 8.
MATLAB indica cual es el número que se encuentra en el renglón 3, columna 2. Para cambiar el número 8 por 5 se asigna de la siguiente forma
C(3,2)=5 C = 1 5 4 3 2 6 9 5 1
Al emplear el operador de dos puntos (:) se pueden realizar operaciones para todo el renglón o la columna que se especifique. Para ilustrar esto escriba el comando y observe los resultados para cada uno de los ejemplos siguientes.
>> C(1,:)
ans =
1 5 4
>> C (:,2)
ans =
5
2
5
Se puede eliminar parte de una matriz o vector asignándole la matriz vacía. Para eliminar el primer renglón se utiliza
>> C (1, : ) = [ ]
C = 3 2 6
9 5 1
Para insertar un renglón se utiliza número de renglones más uno.
>> C (3, : ) = 0
C =
3 2 6
9 8 1
0 0 0
Luego se pueden intercambiar renglones para insertar información
>> C(3,:)= C(1,:)
C =
3 2 6
9 8 1
3 2 6
Finalmente, se agrega la información deseada en el renglón nuevo.
>> C (1,:) = 0
C =
0 0 0
9 8 1
3 2 6
Tarea 2
Defina los siguientes arreglos como matrices