Las expresiones simbólicas son cadenas de caracteres, que representan números, funciones, operadores y variables. Las variables no necesitan tener valores definidos. La aritmética simbólica es el ejercicio de resolver estas ecuaciones simbólicas aplicando reglas e identidades conocidas a los símbolos exactamente en la forma en que se aprendió a resolver en álgebra y cálculo.
En esta sección los comandos y funciones introducidas en esta lección pueden hacer más fácil esto. Ahora a continuación mostramos algunos ejemplos de expresiones simbólicas, junto con su equivalente en MATLAB.
 |  |
 |  |
'1/(2*x^n)'
y = '1/sqrt(2x)'
'cos(x^2) – sin (2*x)'
M = sym ('[a,b;c,d]')
Notarás que en la última expresión se muestra un error.
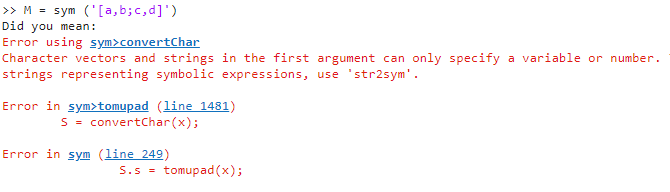
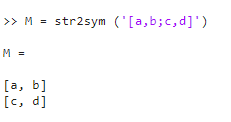
En estos casos, para vectores se debe emplear la función str2sym. La representación ahora es:
APLICACIONES
Las funciones simbólicas de MATLAB permiten manipular expresiones de muchas formas.
Obtener la derivada de cos(x) con respecto a x

La expresión simbólica es definida con la instrucción sym y usando comillas simples para indicarle a MATLAB que ‘cos(x)’ es una cadena de caracteres y dar a entender que se trata de una expresión simbólica, en vez de una expresión numérica.
Dependiendo de la versión de MATLAB que se ocupe, se debe incluir o no la orden sym.
Si no se emplean los paréntesis se obtendrán valores erróneos o no deseados.
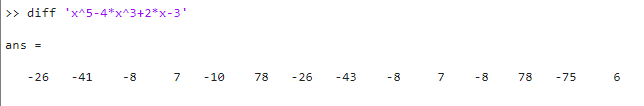
Mientras
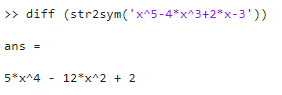
Reglas en las variables simbólicas
Cuando se trabaja con expresiones simbólicas, si la expresión contiene más una variable, sola una de ellas será la variable independiente, si a MATLAB no se le específica cuál es la variable independiente, entonces la selecciona una de acuerdo a las siguientes reglas:
- La variable independiente por defecto de una expresión es la única letra minúscula distinta de i y j, que no es parte de una palabra. Si no existe tal carácter, se elige x. Si el carácter no es único, se elige el más cercano alfabéticamente a x.
- La variable independiente por defecto, conocida algunas veces como la variable libre, en la expresión
‘1 / (5 + cos(x))’
x es la variable.
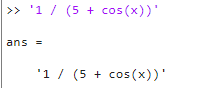
La variable simbólica libre en la expresión ‘sin(pi/4) – cos(3/5)’ es x puesto que esta expresión es una constante simbólica que no tiene variables simbólicas.
la variable libre en la expresión ‘3*y + z’ es y; y la variable libre en la expresión ‘a + sin(t)’ es t.

Usando la función symvar se puede preguntar a MATLAB qué variable de una expresión simbólica se toma como variable independiente.
Ejemplo.
symvar (‘a*x+y’)
symvar(‘a*t+s/(u+3)’)
symvar (‘sin(omega)’)
esto es:

Si usando la regla symvar no puede encontrar una variable simbólica, por defecto se supondrá que no hay ninguna y devuelve a x. Esto siempre se cumple tanto para expresiones que contienen variables de varios caracteres, como constantes simbólicas que no contienen variables.
Ejercicio
Para cada una de las expresiones simbólicas siguientes, use la sintaxis de MATLAB para crear la expresión simbólica equivalente.
A = a*x^2+b*x+c
B = d/dx sqrt(3x^2+2x+5)
C= sqrt(3*x^2+2*x+5)
Ejercicios
Para cada una de las siguientes expresiones, encuentre la variable independiente que devuelva la función symvar.
z=symvar(‘3*a*c+4*b-2’)
f = symvar(‘s^3*n*t’)
x = symvar(‘4*a+3*c+b*b+1’)
n = symvar(‘3*r+2*s^2+5’)
q = symvar(‘r+sqrt(3*k^2+2*p’)
y = symvar (‘tan(3*z)/sin(2*v)-(k/p)’)
Operaciones sobre expresiones simbólicas
Una vez creada una expresión simbólica, probablemente se puede querer combinar de alguna forma, puede ser que se obtenga otra. Si la expresión es un polinomio racional se puede expandir como un polinomio racional, se puede extraer el numerador y el denominador usando la función numden en Matlab. Es importante que no se dejen espacios entre los operadores para que la función no indique errores.
Ejemplo
z =’a*x^2/(b-x)’
[n,m]=numden(str2sym(z))
w = ‘3/2*x^2+2/3*x-3/5’
[n,m]=numden(str2sym(w))
h='(x^2+3)/(2*x-1)+3*x/(x-1)’
[n,m]=numden(str2sym(h))
El resultado es:


Operaciones avanzadas
Matlab tiene la capacidad de realizar más operaciones avanzadas sobre expresiones simbólicas. La función compose combina expresiones, la función finversa obtiene la inversa funcional de una expresión, y la función symsum obtiene la suma simbólica de una expresión.
Dadas las expresiones:
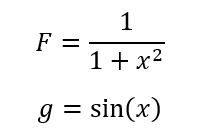
encuentre la expresión compuesta f(g(x)),
compose(str2sym(F),str2sym(g))

compose (str2sym(g),str2sym(F))

y finverse(str2sym(F))
