Búsqueda de raíces
Una actividad común relacionada con las ecuaciones es hallar la solución de la ecuación. La solución es llamada comúnmente la raíz. El objeto del cálculo de las raíces de una ecuación es determinar los valores de x para los que se cumple que f(x) = 0
La determinación de las soluciones de la ecuación f(x) = 0 puede llegar a ser un problema muy sencillo si f(x) es una función polinómica de grado 1 ó 2. Esto es, conocemos expresiones simples que nos permitirán determinar sus raíces.
Para la ecuación y = 2x + 5, en términos de función es f(x) = 2x + 5. Para hallar la raíz sólo se debe aislar x de la función. Así tenemos que 2x + 5 = 0, por lo que
x = – 5/2 ó x = – 2.5
El gráfico muestra encerrado en un círculo rojo la raíz en x = -2.5

para un polinomio de segundo grado y = x2 + 0.3x – 5 sus raíces se obtienen con la fórmula de newton

resolviendo con la fórmula, a = 1, b = 0.3, c = -5;
x1 = (-0.3 + raíz(0.3^2 – 4(1)(-5) ) / 2(1) = (0.3 + raíz(0.09 + 20))/2 = 2.3911
x2 = (-0.3 – raíz(0.3^2 – 4(1)(-5) ) / 2(1) = (0.3 – raíz(20.09))/2 = -4.1822/2 = -2.0911
Para el polinomio de segundo grado hay dos raíces [2.3911 y -2.0911]

De acuerdo al grado de la función se tiene una raíz por cada grado. La función lineal tiene una raíz. La función cuadrática tiene dos raíces.
Para la ecuación cúbica se tienen tres soluciones que puede ser:
- tres raíces reales distintas
- tres raíces reales dos de ellas iguales
- una real y dos complejas
En el caso de las funciones polinomiales se cumple esta regla; sin embargo, para ecuaciones como exp (x), ln(x), sen(x), cos(x), etc. la combinación de términos puede tener o no tener soluciones reales.
Se puede generalizar indicando que si f(x) no es lineal entonces tiene más de una solución o ninguna.
Existen una serie de reglas que pueden ayudar a determinar las raíces de una ecuación:
- El teorema de Bolzano, establece que si una función continua, f(x), toma en los extremos del intervalo [a, b] valores de signo opuesto, entonces la función admite, al menos, una raíz en dicho intervalo. Para pasar de un signo al otro, necesariamente debe cruzar el valor de cero y éste lugar es una raíz o solución.
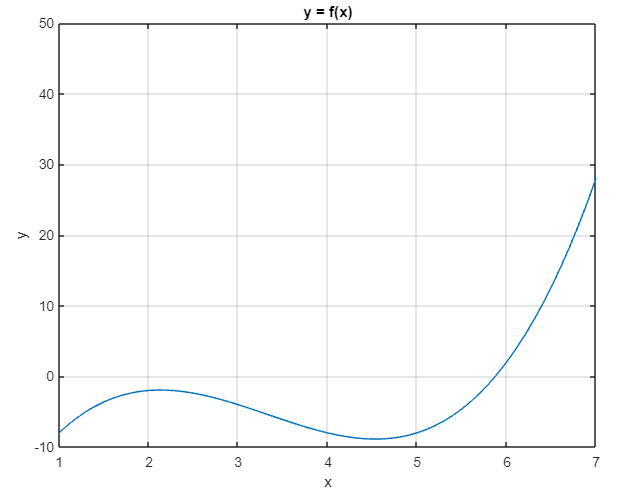
- En el caso en que f(x) sea una función algebraica (polinómica) de grado n y coeficientes reales, podemos afirmar que tendrá n raíces entre reales y complejas.