Modelo de pesca de camarón
La producción de camarón por pesca y acuacultura en el mundo es alrededor de 6 millones 400 mil toneladas de camarón entero y representa divisas superiores a los 20 mil millones de dólares anuales (FAO, 2007).
La especie más abundante es el camarón café y se distribuye en todo el Pacífico mexicano; le siguen en abundancia el camarón azul, concentrado en la costa este de la península de Baja California, Sonora y Sinaloa hasta el Río Piaxtla; del sur del Río Piaxtla hasta el Golfo de Tehuantepec lo sustituye en abundancia el camarón blanco; mientras que el camarón rojo aparece en menor proporción en todas las zonas al sur del Río Piaxtla en Sinaloa (García-Juárez et al., 2014).
Contexto para el modelo en Vensim
Lo siguiente se basa en el trabajo titulado “Quantitative Fisheries Stock Assessment; Choice, Dynamics and Uncertainty” realizado por Hilborn, R y C.J.Walters en 1992.
La pesquería de camarón en México es la tercera pesquería más importante después de la mojarra (cualquiera de varias especies de peces marinos pequeños, plateados, principalmente tropicales americanos) y las ostras en la costa del Golfo de México. En la costa del Pacífico sólo lo superan el atún y la sardina. El valor económico de la captura de camarón la convierte en la pesquería más importante del país, contribuyendo con el 40% del ingreso pesquero total. Los barcos de pescadores de camarón representan el 66% de la flota pesquera actual, mientras que en 1970 representaban el 82%.
En la Bahía de Campeche, al sur del Golfo de México, la especie más importante es el camarón rosado. En la década de 1970 se capturaban más de 20.000 toneladas por año, pero la captura disminuyó constantemente y actualmente es de 4.000 toneladas por año. Los pescadores acusan a PEMEX, la petrolera estatal, de provocar el colapso al invadir y contaminar sus zonas de pesca, aunque la pesca se realiza más al norte y las corrientes marinas concentran la contaminación al sur.
Aunque las estimaciones del gráfico apuntan claramente a una sobreexplotación, ha surgido una interesante controversia entre los investigadores. Uno de los mejores investigadores del país sugirió que si el número de barcos hubiera disminuido, la mortalidad por pesca también debería reducirse. Y, si las capturas no han aumentado, la población está escondida en alguna parte, o si realmente la población ha disminuido, debe ser por otra causa.
Apoyó su argumento con el modelo de Schaeffer (el mismo que el modelo de Verhulst-Pearl, que aplica biomasa en lugar del número de individuos e incluye la pesca) asumiendo que la pesquería está en equilibrio (la captura es igual al crecimiento de la población). En este modelo, si se reduce la actividad de captura, medida por el número de barcos, la población de camarón aumenta.
Sin embargo, se puede argumentar que los barcos que se utilizan actualmente son más potentes que los utilizados a mediados de los años 70, as redes de pesca son más grandes y los viajes más largos (60 días ahora contra 15 días entonces). La población de camarón se concentra ahora en menos lugares y es más vulnerable a la flota. Actualmente sólo existe una cuarta parte del número máximo histórico de barcos. A pesar de ello, el modelo de Schaeffer es el más utilizado. Más que el modelo en sí, el problema podría ser su uso en este caso.
Este modelo tiene la fórmula:
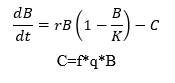
B = Biomasa de la población; r= % de crecimiento de la biomasa; K= mayor Biomasa de población; C = pesca (toneladas o toneladas); f = Esfuerzo pesquero (número de embarcaciones); q = Coeficiente, la fracción de la biomasa capturada por cada unidad de esfuerzo.
Es difícil tener confianza en este modelo, basado en un equilibrio de captura y crecimiento demográfico, cuando los datos observados muestran fuertes diferencia. Usar este modelo equivale a suponer que el efecto observado la captura ha sido igual al crecimiento de la población. esa suposición se originó en la época anterior a las computadoras; su uso simplificó el proceso de determinar los parámetros, permitiendo así completar un análisis de regresión.
En la actualidad, sin embargo, muchos investigadores han abandonado esa suposición y recomiendan en su lugar utilizar métodos que no se basen en un equilibrio (es decir, utilizar métodos que simplemente acepten que la cantidad de captura puede ser diferente del crecimiento de la población).
Datos del modelo
❖ Tiempo Inicial: 1950
❖ Tiempo final: 2000
❖ Unidades de Tiempo: Año
❖ Tipo de Integración: Euler
– Stocks
- Población de camarones = Valor inicial: 30000
- Unidades: toneladas
- Flota pesquera = Valor inicial: 50
- Unidades: barcos
– Flujos
- incremento de la población = tasa de incremento de la biomasa*Población de camarones*(1- (Población de camarones /población máxima))
- Unidades: toneladas/año
- capturas = Capacidad de captura*(Población de camarones/población máxima) *RANDOM NORMAL (0.8, 1.2, 1, 0.1, 5)
- Unidades: toneladas /año
Es función de la capacidad y de la población real en relación a la máxima. Se añade un componente aleatorio para simular fenómenos ocasionales.
- variación de la flota = IF THEN ELSE (margen>0.2, Flota pesquera*coeficiente de adaptación*margen, -Flota pesquera*coeficiente de adaptación*ABS (margen))
- Unidades: barcos/año
Cuando el margen es superior al 20% del coste total se produce un incremento del número de barcos, sino se produce una disminución. La variación de la flota es proporcional al margen real, así es más intensa cuando los márgenes son muy altos.
– Componentes auxiliares
- población máxima = 37500
- Unidades: toneladas
- tasa de incremento de la biomasa = 0.5
- Unidades: 1/año
- Eficacia pesquera = 60+RAMP(3, 1950, 2050)
- Unidades: toneladas/barcos/año
- Capacidad de captura = Flota pesquera*Eficacia pesquera
- Unidades: toneladas/año
- coste/barco = 1
- Unidades: $/barcos/año
- costes totales = Flota pesquera*”coste/barco”
- Unidades: $/año
- ingresos totales = capturas*”precio/Tm”
- Unidades: $/año
- precio/Tm = 0.02
- Unidades: $/toneladas
- margen = (ingresos totales-costes totales) /costes totales
- Unidades: Dmnl
- coeficiente de adaptación = 0.05
- Unidades: 1/año
Si deseas conocer los detalles paso a paso sobre cómo se desarrolló este modelo en Vensim, te invitamos a consultar el PDF al final de esta sección.
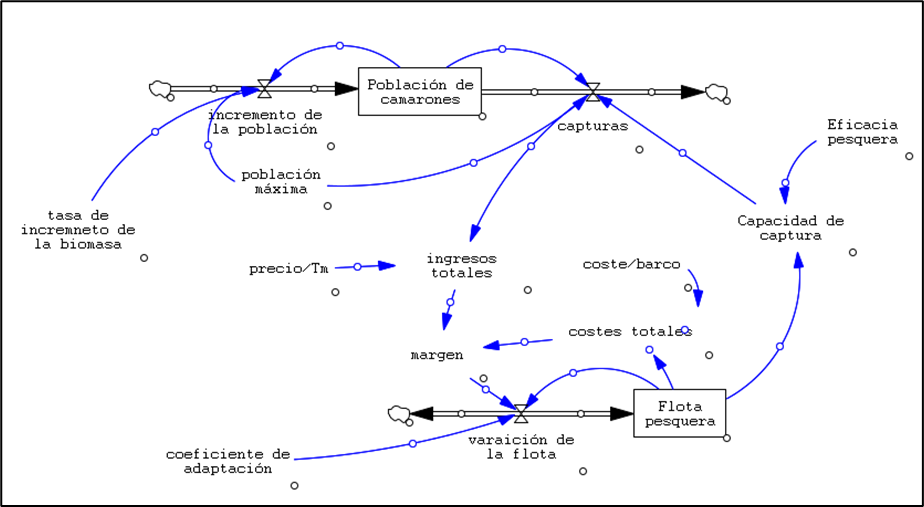
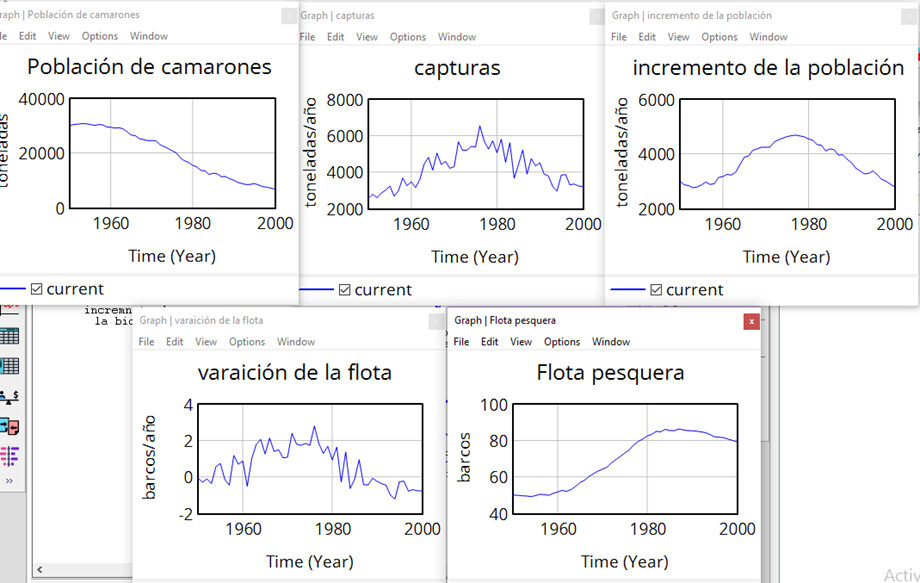
Población de camarones: La población de camarones experimentó un crecimiento significativo durante el período de estudio, aumentando de aproximadamente 20,000 toneladas en 1950 a más de 400,000 toneladas en 2000. El crecimiento no fue constante, sino que se caracterizó por fluctuaciones a lo largo del tiempo. Se observan tres períodos de crecimiento acelerado:
- Entre 1960 y 1970
- Entre 1980 y 1990
- Entre 2000 y 2010
Capturas: Las capturas de camarones aumentaron considerablemente durante el período de estudio, pasando de alrededor de 20,000 toneladas en 1950 a más de 300,000 toneladas en 2000. El patrón de capturas sigue una tendencia similar al de la población de camarones, con períodos de aumento acelerado que coinciden con los de crecimiento de la población.
Incremento de la población: El incremento de la población de camarones muestra una variabilidad significativa a lo largo del tiempo, con períodos de crecimiento positivo y negativo. En general, el incremento de la población fue positivo durante la mayor parte del período de estudio, lo que indica que la población de camarones se encontraba en un estado de crecimiento neto.
Flota pesquera: El tamaño de la flota pesquera experimentó un aumento constante durante el período de estudio, pasando de alrededor de 100 barcos en 1950 a más de 500 barcos en 2000. Este aumento en la flota pesquera coincide con el aumento en las capturas de camarones, lo que sugiere que el esfuerzo pesquero se intensificó durante este período.
Preguntas y ejercicios de retroalimentación.
- ¿Qué sucede con la población de camarones si el número inicial de barcos se incrementa a 100?
- ¿Cómo afecta esto a las capturas y a la variación de la flota a lo largo del tiempo?
- ¿Cómo cambia el comportamiento del modelo si la distribución aleatoria en las capturas (RANDOM NORMAL) tiene una media de 1.1 en lugar de 1?
- ¿Qué patrones observas en la población de camarones y en las capturas cuando varías este componente aleatorio?
- ¿Qué impacto tiene aumentar el coeficiente de adaptación a 0.1 en la variación de la flota pesquera?
Referencias:
- FAO (2007) Anuarios de Estadísticas de pesca. Cuadros resumidos 2005. Producción pesquera: estimación del valor por grupos de especies. 3 p.
- García-Juárez, A., Chávez-Herrera, D., Enciso-Enciso, C. (2014) La pesquería de camarón en el Alto Golfo de California. (Informe Técnico) Instituto Nacional de Pesca.
- Hilborn, R., Walters, C. (1992) “Quantitative Fisheries Stock Assessment; Choice, Dynamics and Uncertainty”. Mathematical methods of population biology. Cambridge University Press.
- Martin, J. (2024) System Dynamics Modelling with Vensim
Modelo de pesca de camarón en Vensim paso a paso