Modelación
La modelación dinámica, actualmente, es una herramienta fundamental en la ecología y las ciencias ambientales. Aplicada a procesos ecológicos implica el desarrollo de modelos matemáticos que representan la dinámica de los sistemas a lo largo del tiempo. Estos modelos se pueden utilizar para comprender cómo interactúan diferentes variables, cómo cambian los ecosistemas bajo diferentes escenarios y cómo responderán a perturbaciones externas, como son las actividades humanas. La dinámica de sistemas, fundamento de la modelación dinámica, es una técnica desarrollada originalmente por Jay W. Forrester del Instituto Tecnológico de Massachusetts a mediados de la década de 1950. Aplicándose ampliamente en diversas áreas, como en economía, finanzas, estudios ambientales, atención médica, tecnología de la información y biología.
Los modelos básicos de los modelación dinámica son el modelo exponencial, el modelo logístico, estos modelos se complementarán para llegar al modelo Presa-Depredador.
Modelo de Malthus (Modelo exponencial)
Este modelo permite representar el crecimiento de una población de organismos que habita en ambiente ilimitado y favorable. A medida que transcurre el tiempo, el número de individuos (Nt) se incrementa cada vez con mayor rapidez hasta que el número de organismos tienda a infinito.
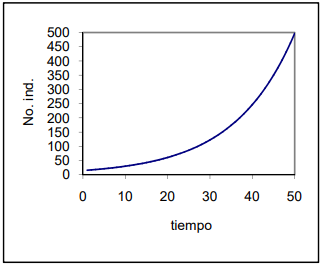
Para describir matemáticamente este comportamiento, debe encontrarse una función f(t) tal que N(t) = f(t). Esto significa que el número de organismos de la población al tiempo t, es una función
del tiempo. En este caso,
f(t) = N0 * ert
Por tanto, la ecuación que lo describe es:
N(t) = N0 * ert
Donde:
N(t) es el número de individuos de la población al tiempo t
N0 es el número de individuos de la población cuando t = 0
r es la tasa intrínseca de crecimiento, que se calcula restando
la tasa de mortalidad (Ds) a la tasa de natalidad (Bs). De esta
forma, r = Bs – Ds
t representa las unidades de tiempo
Modelo de crecimiento logístico
El modelo logístico es un refinamiento del modelo de Malthus. Cuando una magnitud crece en un sistema finito, a partir de cierto punto el tamaño finito del sistema limita el crecimiento de la magnitud al no existir recursos abundantes suficientes para seguir permitiendo el crecimiento exponencial.
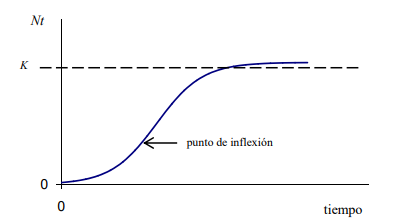
Dicho modelo representa el crecimiento de una población cuando la densidad de la misma ejerce cierta presión sobre la tasa intrínseca de crecimiento, resultando así una curva en forma de S.
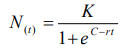
Donde:
K es la “capacidad de carga” del ambiente
C es la constante adquirida en el proceso de integración
N(t) es el número de individuos de la población en el tiempo t
r es el coeficiente que indica la magnitud del potencial
reproductivo de cada individuo
Modelo de Lotka-Volterra (Presa-Depredador)
En cada ecosistema no vive sólo una especie de población. La diversidad de las especies da pie a la competencia por los recursos del medio ambiente. Existe cierta jerarquía a causa de la cadena alimenticia, esta induce los conceptos de presas y depredadores, en el que estos últimos se alimentan
de los primeros para poder sobrevivir. Las ecuaciones de Lotka-Volterra, también conocidas como ecuaciones predador-presa, son un par de ecuaciones diferenciales de primer orden no lineales que se
usan para el modelado de dos poblaciones que interactúan, una presa y un depredador. Las ecuaciones fueron propuestas de forma independiente por Alfred J. Lotka en 1925 y Vito Volterra en 1926.
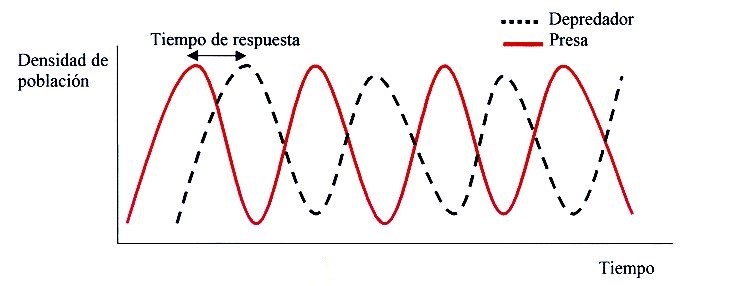
Tales ecuaciones se definen como:
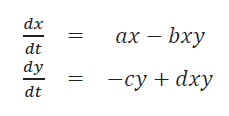
donde:
x = Cantidad de presas al tiempo t.
y = Cantidad de depredadores al tiempo t.
Del modelo de Lotka-Volterra notamos que:
- El término xy modela el número de encuentros entre el
depredador y la presa. - La competencia o la interacción entre las especies está
dada por xy. - Al no existir encuentros entre las especies, los
depredadores tienden a extinguirse. - Cada especie sigue un crecimiento logístico.