También conocido como Modelo de Malthus, este modelo permite representar el crecimiento de una población de organismos que habita en ambiente ilimitado y favorable. A medida que transcurre el tiempo, el número de individuos (Nt) se incrementa cada vez con mayor rapidez hasta que el número de organismos tienda a infinito (Chiappa et al., 2009).

Para describir matemáticamente este comportamiento, debe encontrarse una función f(t) tal que N(t) = f(t). Esto significa que el número de organismos de la población al tiempo t, es una función del tiempo. En este caso,

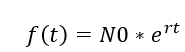
Por tanto, la ecuación que lo describe es:

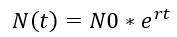
Donde:

N(t) es el número de individuos de la población al tiempo t.

N0 es el número de individuos de la población cuando t = 0.

r es la tasa intrínseca de crecimiento, que se calcula restando la tasa de mortalidad (Ds) a la tasa de natalidad (Bs). De esta forma, r = Bs – Ds

t representa las unidades de tiempo.