Conjuntos

Introducción

Antes de empezar de lleno, recordemos el concepto de conjunto. Según la RAE (Real Academia de la Lengua Española); “Totalidad de los entes matemáticos que tienen una propiedad en común”.

A partir de esas propiedades se desprenden axiomas (principios indemostrables provenientes de un razonamiento deductivo) contenidos en su álgebra. Es importante tener conocimientos previos sobre el tema en cuestión para la correcta interpretación de los resultados arrojados por el programa.

Práctica 1

Relación entre conjuntos (igualdad y desigualdad)

Sean los siguientes conjuntos:

A={x N| x<6}
B={x N| x es divisor de 10}
C={1,2,3,4,5}
D={1,2,5,10}
E={a,e,i,o,u}
F={x| x es una vocal de la palabra riachuelo}

Verifique si son iguales o disjuntos los siguientes pares de conjuntos.

A con C
D con E
B con F
F con D
A con D
E con B
C con E
F con C
A con F
B con D

Solución.

Para la resolución necesitamos comparar ese par de conjuntos, Python puede hacerlo mediante el uso del doble signo igual (“==”), observa la siguiente plantilla, reprodúcela e intenta cambiar algunos parámetros.

Practica 2

Dados los siguientes pares de conjuntos:

V={e}
W={d,e}
X={b,c,d}
Y={b,c}
Z={b,c,e}

Establecer la veracidad o falsedad de las siguientes afirmaciones.

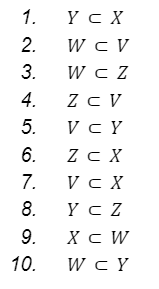
Solución

Para saber si “M” es subconjunto de “N” utilizaremos el siguiente comando: “M.issubset(N)”, en ese mismo orden para que el programa lo identifique, de la forma “N.issubset(M)” se interpreta como “N” es subconjunto de “M”.

Conjunto potencia

En la resolución necesitamos un comando llamado “sorted()” cuya tarea es ordenar de mayor a menor (en caso de contener números en el conjunto a analizar) o en orden alfabético. Utilizaremos la fórmula 2n donde “n” es la cantidad de elementos presentes para determinar si nuestro programa cumple con su objetivo.

Práctica 3

Determine el conjunto potencia y cardinalidad del siguiente conjunto:

A={1,2,3}

Solución

Si aplicamos la fórmula 2n quedaría expresada de la siguiente manera: 23, lo cual da un total de 8, el código realizado debe cumplir con esta regla.

Para contar los elementos mostrados utilizaremos el comando “len()”, aunque cada cada corchete nos indica cada subconjunto

Operaciones entre conjuntos

Conjunto complemento

Se definen como todos los elementos que están en el conjunto universo (U) pero que no están en en el conjunto a analizar. Visto de otra manera:

A’=U-A

Práctica 4

Determine el complemento de los siguientes conjuntos

U={1,2,3,4,5,6,7,8,9,10}
A={1,2,3}

Unión de conjuntos

Para esta operación ocuparemos el siguiente comando: “M.union(N)” o en su defecto utilizaremos la pleca o “|” si el usuario no desea utilizar el comando como tal.

Práctica 5

Dados los siguientes conjuntos realice la operación solicitada:

A=(1,2,3,4,5,6)
B=(-5,-4,-3,-2,-1,0)
C=(11,12,13,14,15,16)
D=(14,15,16,17,18,19)

A U B =
C U D =

Solución

¿Se pueden graficar?

Para graficar sólo se debe agregar códigos para las regiones de los diagramas de Venn a utilizar, nos surgirán errores si no tenemos el conocimiento de el lugar a ocupar de los elementos que conforman.

A continuación se presentan los códigos para los diagramas de dos y tres conjuntos con su respectiva superficie que abarca:

Diagramas de dos conjuntos

“10”: Sólo A (Número 1)
“11”: Intersección de A y B (Número 2)
“01”: Sólo B (Número 3)

Su gráfica y plantilla es la siguiente:

Diagramas de tres conjuntos

La numeración presentada a continuación representa el código para cada uno de los espacios de los diagramas de venn con las intersecciones de tres conjuntos.

“100”: Solo A
“010”: Solo B
“001”: Solo C
“110”: Intersección de A y B
“011”: Intersección de B y C
“101”: Intersección de A y C
“111”: Intersección de A, B y C

Su gráfica y plantilla es la siguiente: