Operaciones entre matrices

Es fácil realizar suma, multiplicación y división entre matrices.

SUMA. La suma de dos matrices de la misma dimensión es aquella matriz cuyos elementos son la suma de los elementos correspondientes.

>> K=[22 14; 46 13]

>>L=[41 27;62 18]

>>K + L


El resultado es

La principal restricción para poder sumar dos matrices es que las matrices deben ser del mismo tamaño (A m×n). No se puede sumar una matriz de 4 x 3 con una de 6 x 2, aun cuando ambas tengan 12 entradas.

---

RESTA. La operación es similar a la suma.

MULTIPLICACIÓN. El producto de una matriz Am×n y una matriz Bn×p es la matriz Cm×p, cuyo elemento en el renglón m y columna p, es la suma de los productos de los elementos correspondientes. A manera de ejemplo.

Sea  A = [1 2 1; 4 1 5]  y  B = [1 2 3; 3 1 -1; 1 4 2]  calcular el producto AB

La operación elemento por elemento es

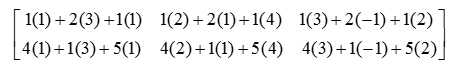
El resultado es

El código y el resultado que se obtiene es

clc

A=[1 2 1;4 1 5]

B=[1 2 3;3 1 -1;1 4 2]

A*B

Para ilustrar otra multiplicación de vectores, ahora defina a los vectores a y b como, a = [ 1 3 3] y b = [4 5 6]’. También defina la matriz A = [1 2 3; 4 3 1; 7 8 9]

>>a = [ 1 3 3]

>>b = [4 5 6]'

>>A = [1 2 3; 4 3 1; 7 8 9]

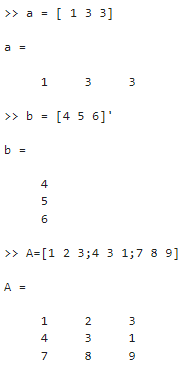
Una vez definidas, realice las operaciones a*b y b*a

>> a*b

ans =
      37

>> b*a


ans =
     4 12 12
     5 15 15
     6 18 18

El primer producto es el producto punto de vectores cuyo resultado es un escalar.

a*b = (1)(4) + (3)(5) + (3)(6) = 37
El segundo producto b*a es el producto cruz cuyo resultado es una matriz.

Después, intenta con a*A o A*b

>> a*A
ans =
     34 35 33

>> A*b
ans =
      32
      37
     122

Estos productos vector-matriz y matriz-vector generan un vector.
¿Qué ocurre cuando las dimensiones no son las requeridas por las operaciones? Para verlo, escriba A*a

>> A*a
Error using * 
Incorrect dimensions for matrix multiplication. Check that the
number of columns in the first matrix matches the number of rows
in the second matrix. To perform elementwise multiplication, use '.*'.

La operación no se realiza debido a que las dimensiones de las matrices son distintas.

La multiplicación matriz-matriz se lleva a cabo de la misma forma que A*A

>> A*A

ans =
30   32     32
23    25    24
102  110   110

También son posibles las operaciones con escalares: A / pi
>> A/pi
ans =
0.3183     0.6366     0.9549
1.2732     0.9549     0.3183
2.2282     2.5465     2.8648

Es importante recordar siempre que MATLAB aplicara las operaciones aritméticas simples en forma de vectores y matrices, si es posible. En ocasiones, se querrá llevar a cabo el cálculo paso por paso en una matriz o vector. MATLAB también puede hacer eso. Por ejemplo, A^2 da como resultado una multiplicación matricial de A = [1 2 3; 4 3 1; 7 8 9] consigo misma. El resultado es A*A

>> A^2

ans =
30   32    32
23    25   24
102  110 110

Pero, ¿Qué hacer si quiere elevar al cuadrado cada elemento de A? Esto se puede hacer con el operador punto de la siguiente manera A .^ 2

>>A.^2

ans =
1       4       9
16      9        1
49     64     81

El punto que precede al operador ^ significa que la operación será llevada a cabo paso por paso (o elemento a elemento). El manual de MATLAB llama a éstas operaciones entre arreglos.
Un uso común de las funciones es evaluar una fórmula o ecuación para una serie de argumentos. Suponga que quiere graficar la función y = 3x²+ 3x – 5 en el intervalo [-1 ,5]. El resultado final debe mostrar la gráfica como la siguiente.

Práctica. Grafique la función 3x² + 3x – 5

Solución. Primero se define el dominio de x.
>> x = linspace ( -1 , 5 );
Después se evalúa la función
>>y =3* x . ^2 + 3*x – 5;
Ahora sólo se grafica con
>> plot (x, y)

Una vez realizada la gráfica de la función no lineal utilizar el comando grid y las etiquetas para complementar mejor la presentación de la gráfica
>> grid on
>> title (‘ y = 3x^2 + 3x – 5’)
>> xlabel (‘x’)
>> ylabel (‘y’)

El resultado corresponde a la gráfica mostrada previamente. Es importante incluir el punto antes del símbolo porque de lo contrario dará un mensaje de error.